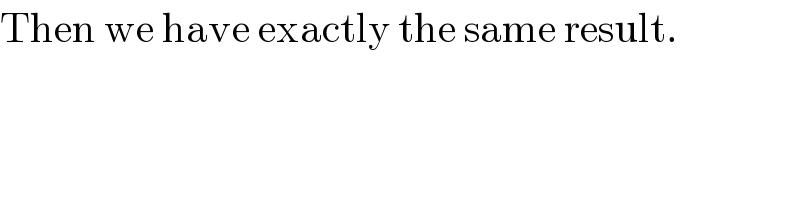Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 15969 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Jun/17

$3 c i r c l e s h a v e t h e s a m e c e n t e r p o i n t .$ $t h e r e i s a e q u i l a t e r a l t r i a n g l e, s u c h t h a t$ $a n y v e r t e x l o c a t e d o n o n e c i r c l e a s s h o w e n .$ $1) h o w c a n w e d r a w s u c h t r i a n g l e ?$ $2) f i n d a r e a o f t h i s t r i a n g l e i n t e r m s o f$ $t h o s e 3 c i r c l e r a d i u s e s .$
Commented by ajfour last updated on 18/Jun/17

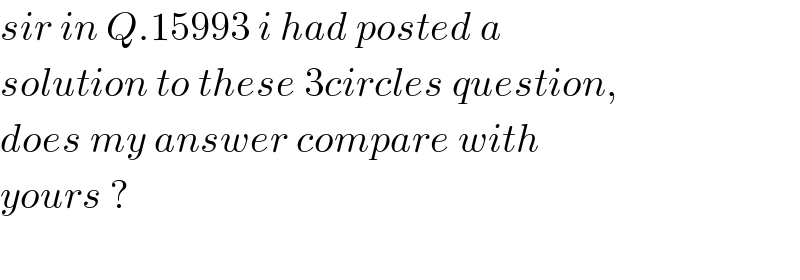
$s i r i n Q . 15993 i h a d p o s t e d a$ $s o l u t i o n t o t h e s e 3 c i r c l e s q u e s t i o n,$ $d o e s m y a n s w e r c o m p a r e w i t h$ $y o u r s ?$
Commented by mrW1 last updated on 17/Jun/17

$When we take a fixed point A on circle 1,$ $and make it as a vertex from an$ $equilateral triangle . The second$ $vertex lies on circle 2 . The track of the$ $third vertex is then also a circle .$ $Using this property we can draw an$ $equilateral triangle on three circles .$ $Fixed point on circle 1 is A .$ $On circle 2 we select some points, at$ $least 3 : P_{1}, P_{2}, P_{3} .$ $We construct 3 equilateral triangles$ $with {AP}_{1}, {AP}_{2}, {AP}_{3} . The third point$ $of the equilateral triangles are Q_{1}, Q_{2}, Q_{3 .}$ $These points should be on the same$ $direction .$ $Through Q_{1}, Q_{2}, Q_{3} a new circle can$ $be constructed . This circle intersects$ $with the circle 3 at point C (as well$ $as C^{'}) . Point C (C^{'}) is the vertex on$ $circle 3 .$ $With point A on circle 1 and C on$ $circle 3 we can easily find the vertex$ $B (as well as B^{'}) on circle 2 .$ $If the fourth circle {doesn}^{'} t intersect$ $with circle 3 it means there is no$ $solution . If it tangents the circle 3 there$ $is only one equilateral triangle, other -$ $wise there are two .$
Commented by mrW1 last updated on 17/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 17/Jun/17

$t h a n k y o u v e r y m u c h m y m a s t e r .$ $i t i s p e r f e c t a n s w e r .$ $i s t h e r e a n y s o l u t i o n b y u s i n g c o m p l e x$ $n u m b e r s ? w h a t d o y o u t h i n k ?$
Commented by RasheedSoomro last updated on 17/Jun/17

$Great knowledge!$
Commented by mrW1 last updated on 19/Jun/17

$I got the formula to calculate the side$ $length of the equilateral triangle$ $analytically .$ $Radius of circle 1 = a > 0$ $Radius of circle 2 = b$ $Radius of circle 3 = c$ $let β = \frac{b}{a}, γ = \frac{c}{a}$ $The condition that such triangle (s)$ $exists is a ⩽ c ⩽ a + b .$ $The length of sides of the triangle is$ $d = \frac{a}{2} \sqrt{λ^{2} + {(\sqrt{δ} \pm \sqrt{3})}^{2}}$ $with$ $λ = (γ + β) (γ - β)$ $δ = (γ + β + 1) (1 + β - γ) (γ - β + 1) (γ + β - 1)$ $The area of the equilateral triangle is$ $A = \frac{\sqrt{3}}{4} d^{2} = \frac{\sqrt{3} a^{2}}{16} [λ^{2} + {(\sqrt{δ} \pm \sqrt{3})}^{2}]$
Commented by mrW1 last updated on 18/Jun/17

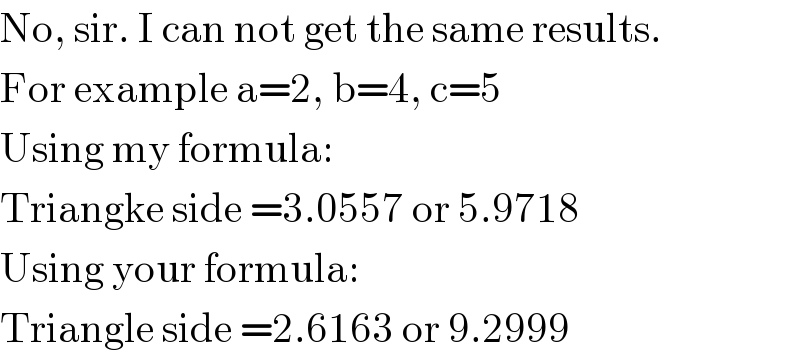
$No, sir . I can not get the same results .$ $For example a = 2, b = 4, c = 5$ $Using my formula :$ $Triangke side = 3.0557 or 5.9718$ $Using your formula :$ $Triangle side = 2.6163 or 9.2999$
Commented by ajfour last updated on 18/Jun/17

$o k a y s i r, i w i l l c h e c k m y s o l u t i o n$ $a n d a n s w e r, t h a n k s f o r a n$ $e x a m p l e t o c o m p a r e .$
Commented by ajfour last updated on 19/Jun/17

$a m e n d e d m y r e s u l t s i r,$ $d^{2} = \frac{1}{2} (a^{2} + b^{2} + c^{2})$ $\pm \frac{\sqrt{3}}{2} \sqrt{2 (a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}) - (a^{4} + b^{4} + c^{4})}$ $w i t h a = b = c i t g i v e s c o r r e c t$ $a n s w e r, e v e n f o r a = 2, b = 4, c = 5$ $t h e a n s w e r m a t c h e s w i t h y o u r s,$ $b u t o u r e x p r e s s i o n s f o r s i d e$ $l e n g t h d o n t c o n v e r t (n o t b y m e) .$ $h o w e v e r i n b o t h t h e s e c a s e s y o u r$ $c o n d i t i o n c ⩾ a + b, d o n t h o l d t r u e .$ $k i n d l y v e r i f y t h i s, S i r .$
Commented by mrW1 last updated on 19/Jun/17

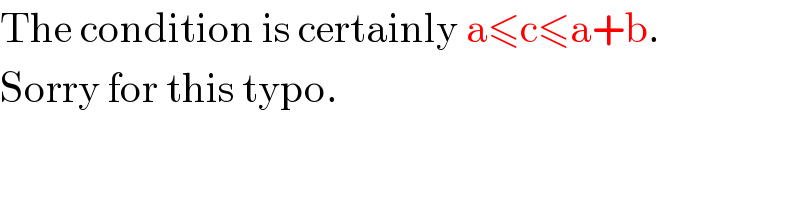
$The condition is certainly a ⩽ c ⩽ a + b .$ $Sorry for this typo .$
Commented by ajfour last updated on 19/Jun/17

$w h a t a b o u t c h e c k i n g m y e x p r e s s i o n$ $f o r s i d e l e n g t h o f Δ, S i r; f o r i t$ $q u a l i f i e s w e l l a n d i s p r e c i s e$ $e n o u g h . . k i n d l y v i e w m y s o l u t i o n$ $w h e n i p o s t i t a g a i n, i t m i g h t t a k e$ $t w o h o u r s, i t h i n k .$
Commented by mrW1 last updated on 19/Jun/17

$sir, what is d in this expression ?$ $d^{2} = \frac{1}{2} (a^{2} + b^{2} + c^{2})$ $\pm \frac{\sqrt{3}}{2} \sqrt{2 (a^{2} + b^{2} + c^{2}) - (a^{4} + b^{4} + c^{4})}$ $with a = 2, b = 4, c = 5 we have$ $\sqrt{2 (a^{2} + b^{2} + c^{2}) - (a^{4} + b^{4} + c^{4})}$ $= \sqrt{2 (2^{2} + 4^{2} + 5^{2}) - (2^{4} + 4^{4} + 5^{4})}$ $= \sqrt{- 807}$ $this is not real .$ $please check sir .$ $for comparation please give me$ $your expression for side length of$ $the triangle which is d in my formula .$
Commented by mrW1 last updated on 19/Jun/17

$further simplification :$ $λ = (γ + β) (γ - β)$ $δ = (γ + β + 1) (1 + β - γ) (γ - β + 1) (γ + β - 1)$ $δ = [{(1 + β)}^{2} - γ^{2}] [γ^{2} - {(β - 1)}^{2}]$ $= {(β + 1)}^{2} γ^{2} - γ^{4} - {(β + 1)}^{2} {(β - 1)}^{2} + {(β - 1)}^{2} γ^{2}$ $= [{(β + 1)}^{2} + {(β - 1)}^{2}] γ^{2} - γ^{4} - {(β + 1)}^{2} {(β - 1)}^{2}$ $= 2 (β^{2} + 1) γ^{2} - γ^{4} - β^{4} + 2 β^{2} - 1$ $= 2 β^{2} γ^{2} + 2 γ^{2} - γ^{4} - β^{4} + 2 β^{2} - 1$ $= 2 (β^{2} γ^{2} + β^{2} + γ^{2}) - (1 + γ^{4} + β^{4})$ $λ^{2} = {(γ^{2} - β^{2})}^{2} = γ^{4} + β^{4} - 2 β^{2} γ^{2}$ $λ^{2} + {(\sqrt{δ} \pm \sqrt{3})}^{2} = λ^{2} + δ + 3 \pm 2 \sqrt{3 δ}$ $= γ^{4} + β^{4} - 2 β^{2} γ^{2} + 2 β^{2} γ^{2} + 2 γ^{2} - γ^{4} - β^{4} + 2 β^{2} - 1 + 3 \pm 2 \sqrt{3 δ}$ $= 2 γ^{2} + 2 β^{2} + 2 \pm 2 \sqrt{3 δ}$ $= 2 (1 + γ^{2} + β^{2} \pm \sqrt{3 δ})$ $d = \frac{a}{\sqrt{2}} \sqrt{1 + β^{2} + γ^{2} \pm \sqrt{3 δ}}$ $d = \frac{a}{\sqrt{2}} \sqrt{(1 + β^{2} + γ^{2}) \pm \sqrt{3} \times \sqrt{2 (β^{2} + γ^{2} + β^{2} γ^{2}) - (1 + β^{4} + γ^{4})}}$ $or$ $d = \frac{1}{\sqrt{2}} \sqrt{(a^{2} + b^{2} + c^{2}) \pm \sqrt{6 (a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}) - 3 (a^{4} + b^{4} + c^{4})}}$ $A = \frac{\sqrt{3}}{4} d^{2} = \frac{\sqrt{3}}{8} [a^{2} + b^{2} + c^{2} \pm \sqrt{6 (a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2}) - 3 (a^{4} + b^{4} + c^{4})}]$
Commented by mrW1 last updated on 19/Jun/17

$To mr . alfour :$ $I think your formula should be$ $d^{2} = \frac{1}{2} (a^{2} + b^{2} + c^{2})$ $\pm \frac{\sqrt{3}}{2} \sqrt{{2 a}^{2} (b^{2} + c^{2}) + {2 b}^{2} c^{2} - (a^{4} + b^{4} + c^{4})}$
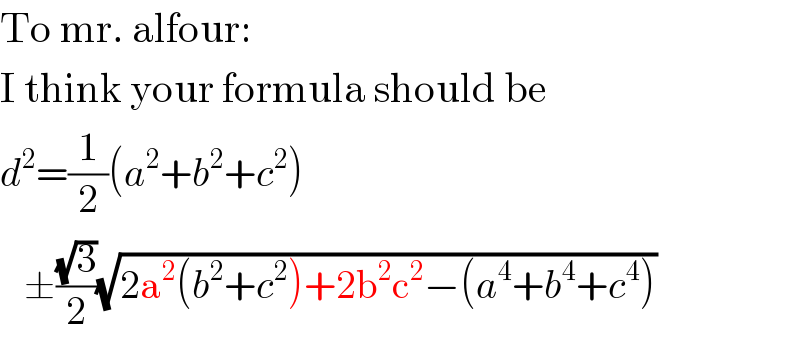
Commented by ajfour last updated on 19/Jun/17

$y e s s i r, i t w a s t h i s i n m y n o t e b o o k$ $b u t w h e n i t y p e d i t t o y o u i t h o u g h t$ $i r e m e m b e r e d a n d t y p e d w r o n g$ $i n s t e a d . . T h a n k y o u s i r .$ $d i s t h e s a m e t h i n g - s i d e l e n g t h .$
Commented by mrW1 last updated on 19/Jun/17

$Then we have exactly the same result .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum