
Question and Answers Forum
Question Number 160496 by mathlove last updated on 30/Nov/21

Answered by Kamel last updated on 01/Dec/21
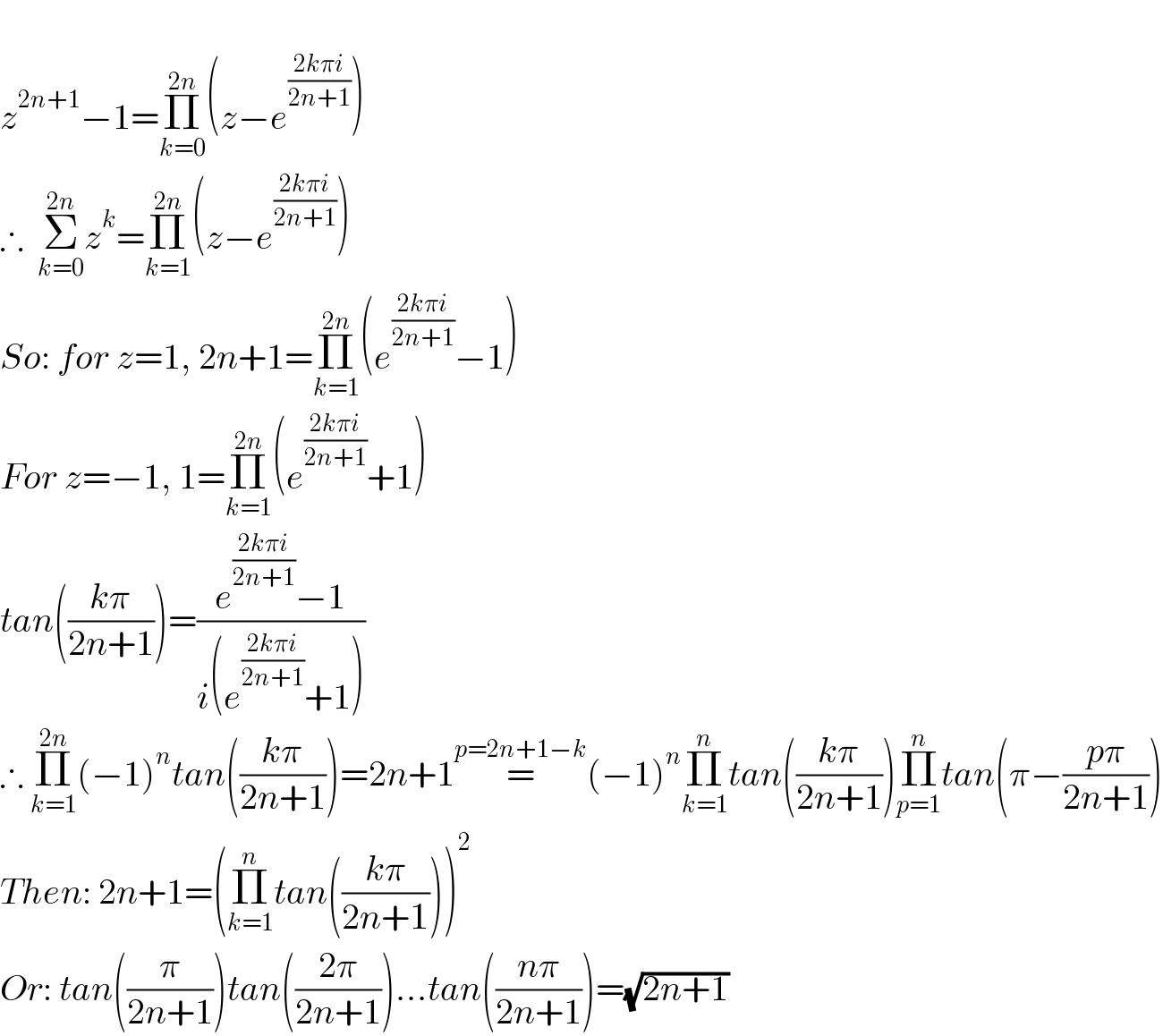
Answered by mr W last updated on 30/Nov/21
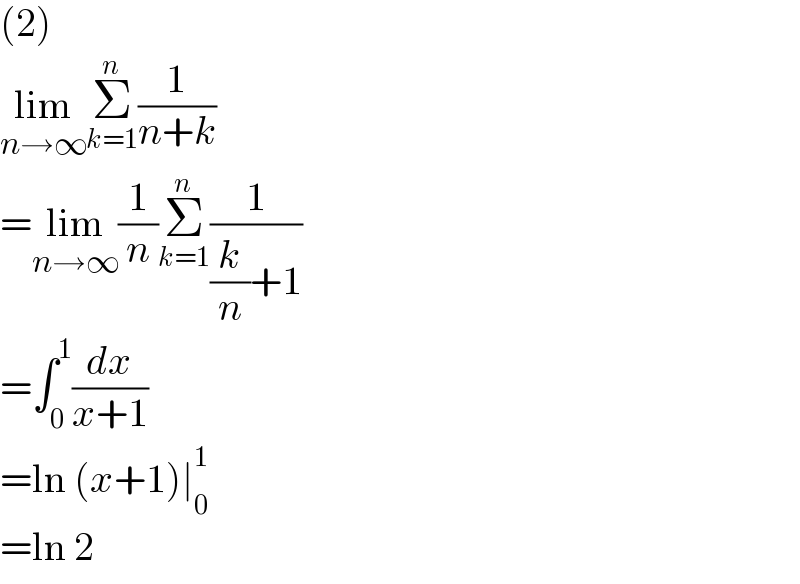
| ||
Question and Answers Forum | ||
Question Number 160496 by mathlove last updated on 30/Nov/21 | ||
 | ||
Answered by Kamel last updated on 01/Dec/21 | ||
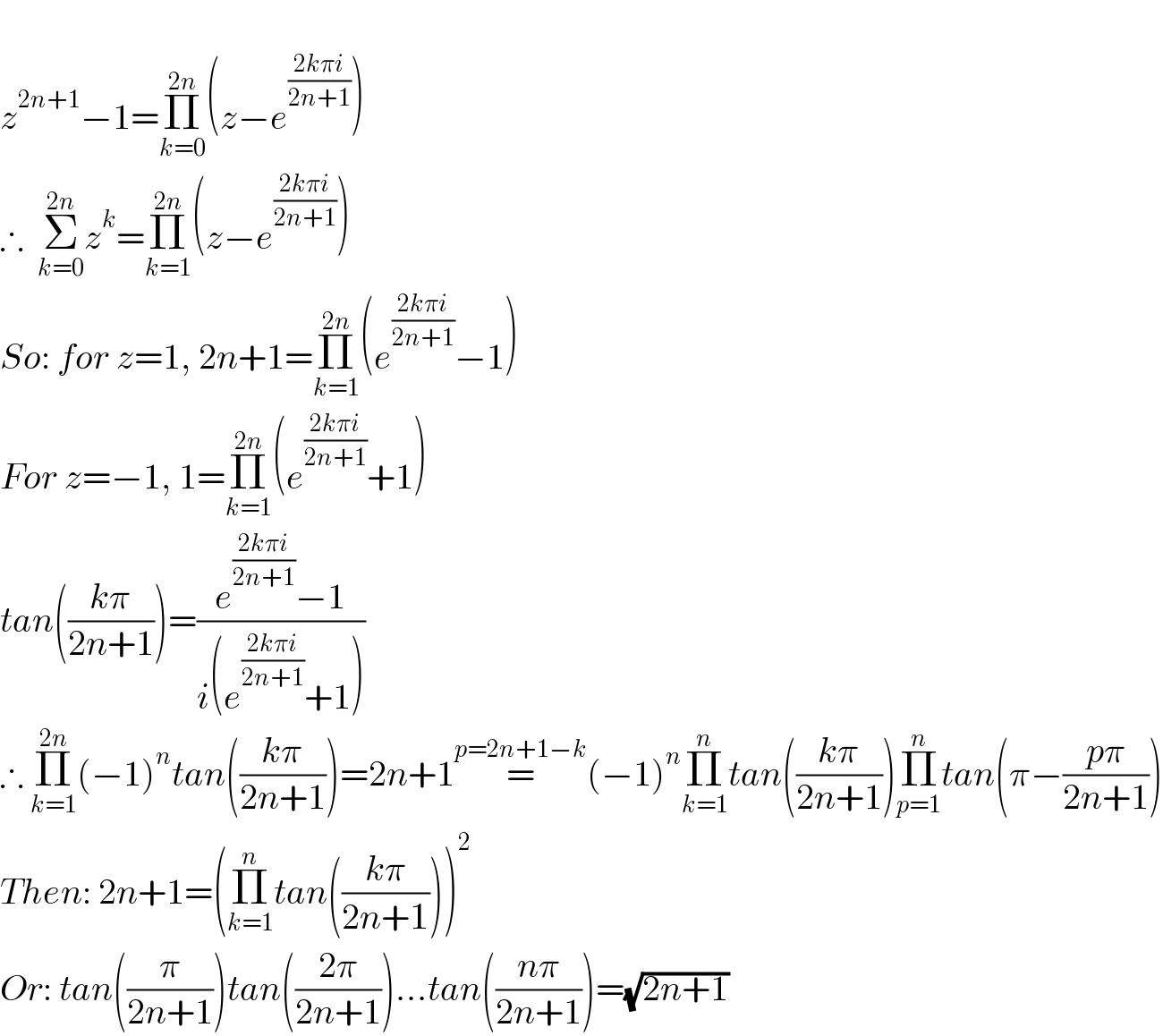 | ||
| ||
Answered by mr W last updated on 30/Nov/21 | ||
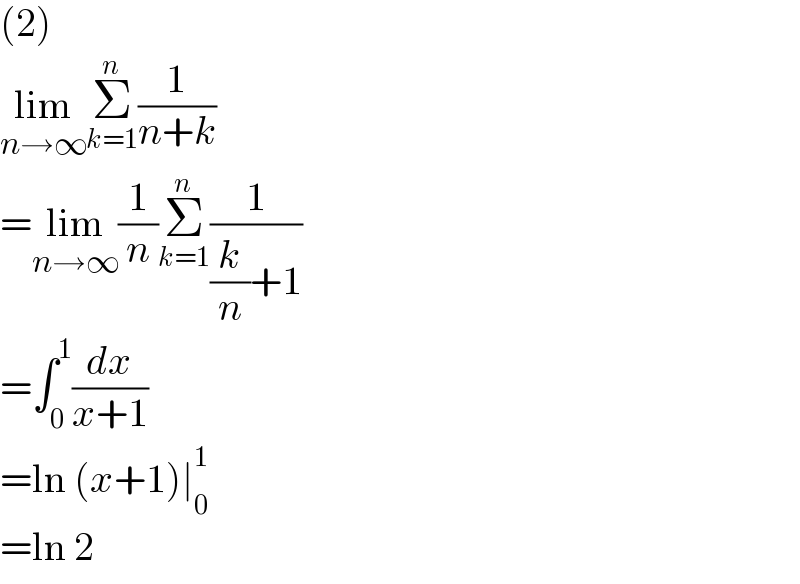 | ||
| ||