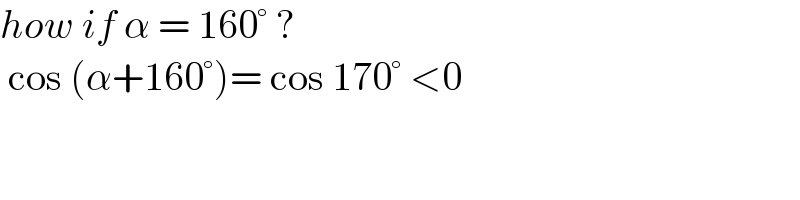Question and Answers Forum
Question Number 161322 by kapoorshah last updated on 16/Dec/21
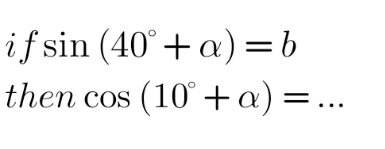
Commented by cortano last updated on 16/Dec/21
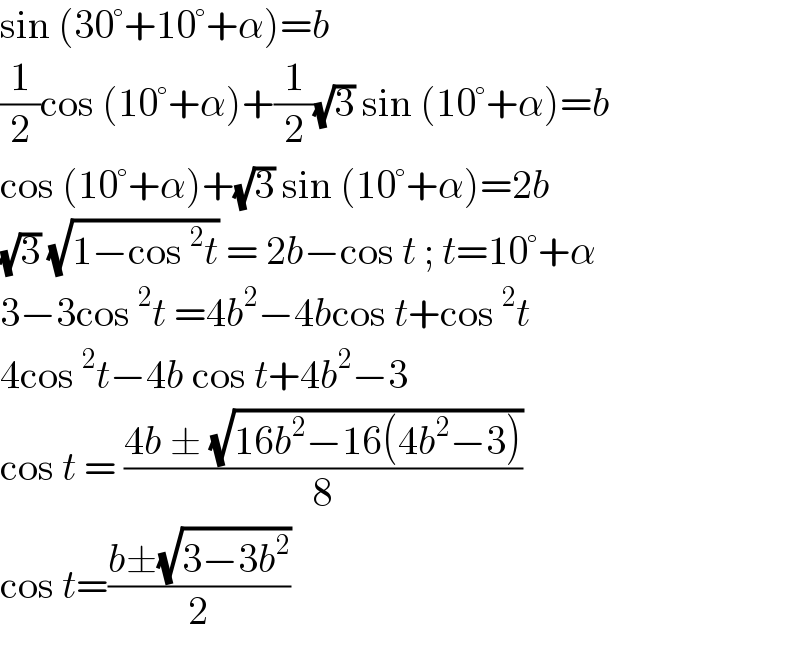
Commented by MJS_new last updated on 16/Dec/21
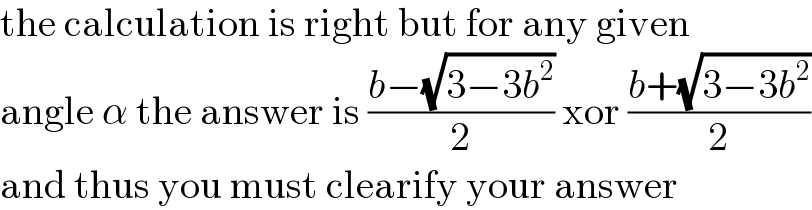
Commented by cortano last updated on 16/Dec/21
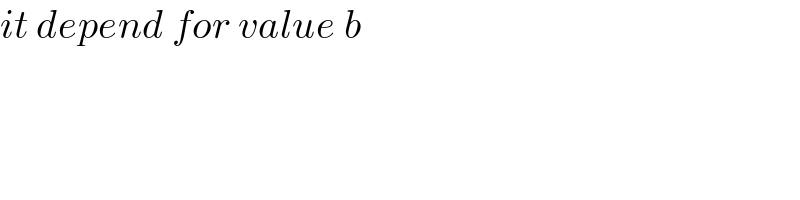
Commented by MJS_new last updated on 17/Dec/21
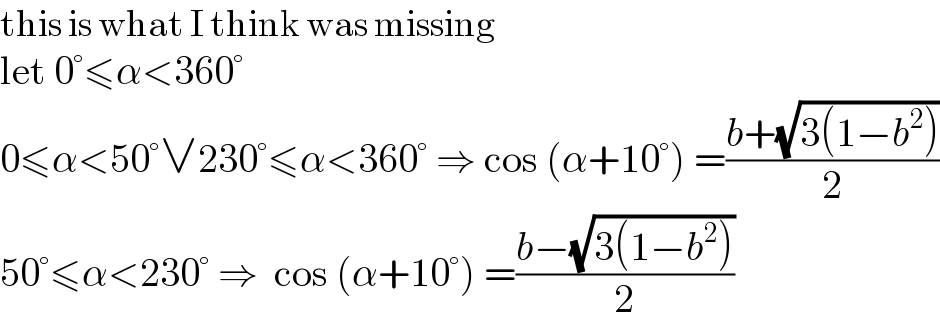
Answered by 1549442205PVT last updated on 16/Dec/21
![sin(40^0 +α)=sin[30^0 +(10^0 +α)] =sin30^0 cos(10^0 +α)+cos30^0 sin(10^0 +α) =(1/2)cos(10^0 +α)+((√3)/2)sin(10^0 +α)=b we have the system of equations: { ((x+(√3)y=2b)),((x^2 +y^2 =1)) :}with x=cos(10^0 +α),y=sin(10^0 +α) ⇒(2b−(√3)y)^2 +y^2 =1⇔4y^2 −4b(√3)y+4b^2 −1=0 △′=12b^2 −16b^2 +4=4−4b^2 .Hence y=((2b(√3)±2(√(1−b^2 )))/4).From that x=cos(10^0 +α)=b−(√3)y=2b−((6b±2(√(3−3b^2 )))/4) =((2b±2(√(3−3b^2 )))/4)=((b±(√(3−3b^2 )))/2)](Q161327.png)
Commented by 1549442205PVT last updated on 16/Dec/21
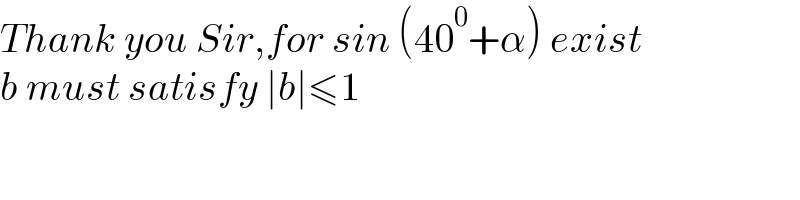
Commented by MJS_new last updated on 16/Dec/21
Commented by mr W last updated on 16/Dec/21
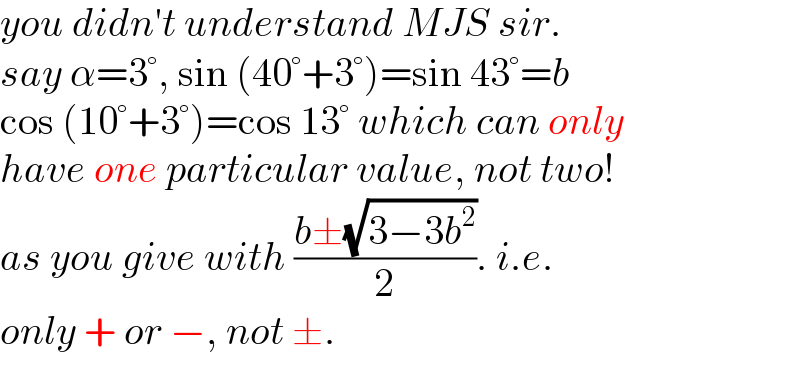
Commented by cortano last updated on 17/Dec/21