Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 161773 by smallEinstein last updated on 22/Dec/21

Commented by Tawa11 last updated on 22/Dec/21

$$\mathrm{Sir}\mathrm{einstein},\mathrm{please}\mathrm{what}\mathrm{is}\mathrm{the}\mathrm{name}\mathrm{of}\mathrm{this}\mathrm{app}?$$

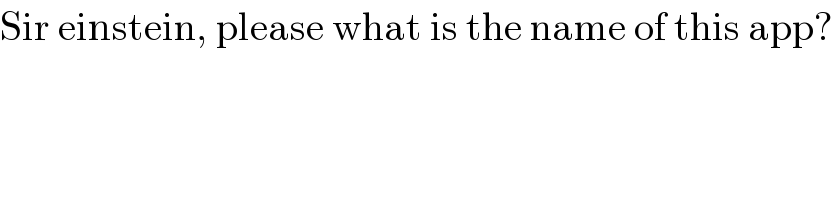
Answered by Ar Brandon last updated on 22/Dec/21

$$I={\int }_0^{\mathrm{\infty }}{x}^2{e}^{-2x}\sin \left(2x\right)\ln xdx=\frac{\partial }{\partial \alpha }{\mid }_{\alpha =2}{\int }_0^{\mathrm{\infty }}{x}^{\alpha }{e}^{-2x}\sin \left(2x\right)dx$$$$=\frac{\partial }{\partial \alpha }{\mid }_{\alpha =2}\frac{1}{2^{\alpha +1}}{\int }_0^{\mathrm{\infty }}{t}^{\alpha }{e}^{-t}\sin \left(t\right)dt=\frac{\partial }{\partial \alpha }{\mid }_{\alpha =2}\frac{1}{2^{\alpha +1}}{\int }_0^{\mathrm{\infty }}{t}^{\alpha }{e}^{-t}\left(\frac{e^{it}-e^{-it}}{2i}\right)dt$$$$=\frac{\partial }{\partial \alpha }{\mid }_{\alpha =2}\frac{i}{2^{\alpha +2}}{\int }_0^{\mathrm{\infty }}{t}^{\alpha }(e^{-(1+i)t}-e^{-(1-i)t})dt$$$$=\frac{\partial }{\partial \alpha }{\mid }_{\alpha =2}\frac{i}{2^{\alpha +2}}[{\int }_0^{\mathrm{\infty }}{t}^{\alpha }{e}^{-(1+i)t}dt-{\int }_0^{\mathrm{\infty }}{t}^{\alpha }{e}^{-(1-i)t}dt]$$$$=\frac{\partial }{\partial \alpha }{\mid }_{\alpha =2}\frac{i}{2^{\alpha +2}}[\frac{1}{{(1+i)}^{\alpha +1}}{\int }_0^{\mathrm{\infty }}{u}^{\alpha }{e}^{-u}du-\frac{1}{{(1-i)}^{\alpha +1}}{\int }_0^{\mathrm{\infty }}{v}^{\alpha }{e}^{-v}dv$$$$=\frac{\partial }{\partial \alpha }{\mid }_{\alpha =2}\frac{i}{2^{\alpha +2}}[\frac{\mathrm{\Gamma }(\alpha +1)}{{(1+i)}^{\alpha +1}}-\frac{\mathrm{\Gamma }(\alpha +1)}{{(1-i)}^{\alpha +1}}]=\frac{i}{2}\cdot \frac{\partial }{\partial \alpha }{\mid }_{\alpha =2}[\frac{1}{{(2+2i)}^{\alpha +1}}-\frac{1}{{(2-2i)}^{\alpha +1}}]\mathrm{\Gamma }(\alpha +1)$$$$=\frac{i}{2}\cdot {\mid }_{\alpha =2}(\frac{1}{{(2+2i)}^{\alpha +1}}-\frac{1}{{(2-2i)}^{\alpha +1}}){\mathrm{\Gamma }}^{\prime }(\alpha +1)+(\frac{\ln (2-2i)}{{(2-2i)}^{\alpha +1}}-\frac{\ln (2+2i)}{{(2+2i)}^{\alpha +1}})\mathrm{\Gamma }(\alpha +1)$$$$=\frac{i}{2}[(\frac{1}{{(2+2i)}^3}-\frac{1}{{(2-2i)}^3}){\mathrm{\Gamma }}^{\prime }\left(3\right)+(\frac{\ln (2-2i)}{{(2-2i)}^3}-\frac{\ln (2+2i)}{{(2+2i)}^3})\mathrm{\Gamma }\left(3\right)$$$$=\frac{i}{2}[\left(\frac{8e^{-\frac{3}{4}i\pi }-8e^{\frac{3}{4}i\pi }}{512}\right)\mathrm{\Gamma }\left(3\right)\psi \left(3\right)+\left(\frac{8e^{\frac{3}{4}i\pi }\ln 2e^{-\frac{\pi }{4}i}-8e^{-\frac{3}{4}i\pi }\ln 2e^{\frac{\pi }{4}i}}{512}\right)\mathrm{\Gamma }\left(3\right)]$$$$=\frac{i}{64}(-2i\sin \left(\frac{3\pi }{4}\right))(\frac{3}{2}-\gamma )+\frac{i}{64}(e^{\frac{3}{4}i\pi }(\ln 2-\frac{\pi }{4}i)-e^{-\frac{3}{4}i\pi }(\ln 2+\frac{\pi }{4}i))$$$$=\frac{\sqrt{2}}{64}(\frac{3}{2}-\gamma )+\frac{i}{64}((e^{\frac{3}{4}i\pi }-e^{-\frac{3}{4}i\pi })\ln 2-\frac{\pi }{4}(e^{\frac{5}{4}i\pi }+e^{-\frac{1}{4}i\pi }))$$$$=\frac{\sqrt{2}}{64}(\frac{3}{2}-\gamma )-\frac{1}{32}\sin \left(\frac{3\pi }{4}\right)\ln 2+\frac{\pi }{256}i\left(2i\sin \left(\frac{\pi }{4}\right)\right)$$$$=\frac{\sqrt{2}}{64}(\frac{3}{2}-\gamma )-\frac{\sqrt{2}}{64}\ln 2-\frac{\pi \sqrt{2}}{256}=-\frac{\pi }{128\sqrt{2}}-\frac{1}{32\sqrt{2}}\gamma -\frac{1}{32\sqrt{2}}\ln 2+\frac{3}{64\sqrt{2}}$$$$Stillcheckingfortypos$$

Answered by Lordose last updated on 22/Dec/21

$$$$$$\mathrm{I}={\int }_0^{\mathrm{\infty }}{\mathrm{x}}^2{\mathrm{e}}^{-2\mathrm{x}}\sin \left(2\mathrm{x}\right)\ln \left(\mathrm{x}\right)\mathrm{dx}$$$$\mathrm{I}=\frac{\partial }{\partial \mathrm{a}}{\mid }_{\mathrm{a}=2}{\int }_0^{\mathrm{\infty }}{\mathrm{x}}^{\mathrm{a}}{\mathrm{e}}^{-2\mathrm{x}}\sin \left(2\mathrm{x}\right)\mathrm{dx}$$$$\mathrm{I}\stackrel{\mathrm{x}=\frac{\mathrm{x}}{2}}{=}\frac{\partial }{\partial \mathrm{a}}{\mid }_{\mathrm{a}=2}\frac{1}{2^{\mathrm{a}+1}}{\int }_0^{\mathrm{\infty }}{\mathrm{x}}^{\mathrm{a}}{\mathrm{e}}^{-\mathrm{x}}\sin \left(\mathrm{x}\right)\mathrm{dx}$$$$\mathrm{I}=\mathfrak{Im}\frac{\partial }{\partial \mathrm{a}}{\mid }_{\mathrm{a}=2}\frac{1}{2^{\mathrm{a}+1}}{\int }_0^{\mathrm{\infty }}{\mathrm{x}}^{\mathrm{a}}{\mathrm{e}}^{-\mathrm{x}(1-\mathbf{i})}\mathrm{dx}$$$$\mathrm{I}\stackrel{\mathrm{x}=\mathrm{x}(1-\mathbf{i})}{=}\mathfrak{Im}\frac{\partial }{\partial \mathrm{a}}{\mid }_{\mathrm{a}=2}\frac{1}{2^{\mathrm{a}+1}{(1-\mathrm{i})}^{\mathrm{a}+1}}{\int }_0^{\mathrm{\infty }}{\mathrm{x}}^{\mathrm{a}+1-1}{\mathrm{e}}^{-\mathrm{x}}\mathrm{dx}$$$$\mathrm{I}=\mathfrak{Im}\frac{\partial }{\partial \mathrm{a}}{\mid }_{\mathrm{a}=2}\frac{\mathbf{\Gamma }(\mathrm{a}+1)}{2^{\mathrm{a}+1}{(1-\mathrm{i})}^{\mathrm{a}+1}}$$$$\mathrm{I}=\mathfrak{Im}\mid \frac{\mathit{\psi }(\mathrm{a}+1)\mathbf{\Gamma }(\mathrm{a}+1)}{2^{\mathrm{a}+1}{(1-\mathbf{i})}^{\mathrm{a}+1}}-\frac{\mathbf{\Gamma }(\mathrm{a}+1)\ln \left(2\right)+\mathbf{\Gamma }(\mathrm{a}+1)\ln (1-\mathrm{i})}{2^{\mathrm{a}+1}{(1-\mathbf{i})}^{\mathrm{a}+1}}{\mid }_{\mathrm{a}=2}$$$$\mathrm{I}=\mathfrak{Im}(\frac{\mathit{\psi }\left(3\right)\mathbf{\Gamma }\left(3\right)}{2^3{(1-\mathbf{i})}^3}-\frac{\mathbf{\Gamma }\left(3\right)\ln \left(2\right)+\mathbf{\Gamma }\left(3\right)\ln (1-\mathbf{i})}{2^3{(1-\mathbf{i})}^3})$$$$\mathrm{I}=\mathfrak{Im}\left(\frac{1}{64}(4\mathit{\gamma }+\mathit{\pi }-2(3+\ln \left(8\right))+\mathrm{i}(6-4\mathit{\gamma }-\mathit{\pi }-\ln \left(64\right)))\right)$$$$\mathrm{I}=\frac{1}{64}(6-4\mathit{\gamma }-\mathit{\pi }-6\ln \left(2\right))$$

Commented by Ar Brandon last updated on 22/Dec/21

$$\mathrm{Nice}$$

Answered by mathmax by abdo last updated on 23/Dec/21

$$\mathrm{f}\left(\mathrm{a}\right)={\int }_0^{\mathrm{\infty }}{\mathrm{x}}^{\mathrm{a}+2}{\mathrm{e}}^{-\mathrm{x}-2}\sin \left(2\mathrm{x}\right)\mathrm{dx}$$$$\mathrm{f}\left(\mathrm{a}\right)=\mathrm{Im}\left({\int }_0^{\mathrm{\infty }}{\mathrm{x}}^{\mathrm{a}+2}{\mathrm{e}}^{-\mathrm{x}-2+2\mathrm{ix}}\mathrm{dx}\right)$$$$\mathrm{and}{\int }_0^{\mathrm{\infty }}{\mathrm{x}}^{\mathrm{a}+2}{\mathrm{e}}^{-2+(2\mathrm{i}-1)\mathrm{x}}\mathrm{dx}{=}_{(2\mathrm{i}-1)\mathrm{x}=-\mathrm{t}}$$$${\int }_0^{\mathrm{\infty }}{\left(\frac{-\mathrm{t}}{2\mathrm{i}-1}\right)}^{\mathrm{a}+2}{\mathrm{e}}^{-2-\mathrm{t}}\frac{-\mathrm{dt}}{(2\mathrm{i}-1)}$$$$={\mathrm{e}}^{-2}{\left(\frac{1}{2\mathrm{i}-1}\right)}^{\mathrm{a}+3}{(-1)}^{\mathrm{a}+2}{\int }_0^{\mathrm{\infty }}{\left(\mathrm{t}\right)}^{\mathrm{a}+2}{\mathrm{e}}^{-\mathrm{t}}\mathrm{dt}$$$$=\frac{{\mathrm{e}}^{-2}{(-1)}^{\mathrm{a}}}{{(2\mathrm{i}-1)}^{\mathrm{a}+3}}\times \mathrm{\Gamma }(\mathrm{a}+3)$$$${\mathrm{f}}^{{}^{\prime }}\left(\mathrm{a}\right)={\int }_0^{\mathrm{\infty }}{\mathrm{x}}^2{\left({\mathrm{e}}^{\mathrm{alogx}}\right)}^{{}^{\prime }}{\mathrm{e}}^{-\mathrm{x}-2}\sin \left(2\mathrm{x}\right)\mathrm{dx}$$$$={\int }_0^{\mathrm{\infty }}{\mathrm{x}}^2\mathrm{logx}{\mathrm{x}}^{\mathrm{a}}{\mathrm{e}}^{-\mathrm{x}-2}\sin \left(2\mathrm{x}\right)\mathrm{dx}$$$$\Rightarrow {\mathrm{f}}^{{}^{\prime }}\left(0\right)={\int }_0^{\mathrm{\infty }}{\mathrm{x}}^2{\mathrm{e}}^{-\mathrm{x}-2}\sin \left(2\mathrm{x}\right)\mathrm{logx}\mathrm{dx}$$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{{\mathrm{e}}^{-2}}{{(2\mathrm{i}-1)}^3}{(-\frac{1}{2\mathrm{i}-1})}^{\mathrm{a}}.\mathrm{\Gamma }(\mathrm{a}+3)$$$$=\frac{{\mathrm{e}}^{-2}}{(\sqrt{5}{\mathrm{e}}^{-\mathrm{iarctan}\left(2\right)}3}{(-\frac{1}{\sqrt{5}{\mathrm{e}}^{-\mathrm{iarctan}2}})}^{\mathrm{a}}.\mathrm{\Gamma }(\mathrm{a}+3)$$$$={(-1)}^{\mathrm{a}}{\mathrm{e}}^{-2}{\left(\frac{1}{\sqrt{5}{\mathrm{e}}^{-\mathrm{iarctan}2}}\right)}^{\mathrm{a}}.\mathrm{\Gamma }(\mathrm{a}+3)$$$$={\mathrm{e}}^{\mathrm{i}\pi \mathrm{a}}{\mathrm{e}}^{-2}{5}^{\frac{\mathrm{a}}{2}}{\mathrm{e}}^{\mathrm{iaarctan}2}.\mathrm{\Gamma }(\mathrm{a}+3)\mathrm{rest}\mathrm{to}\mathrm{calculate}{\mathrm{f}}^{{}^{\prime }}\left(0\right)....\mathrm{be}\mathrm{continued}...$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com