Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 161912 by mr W last updated on 24/Dec/21

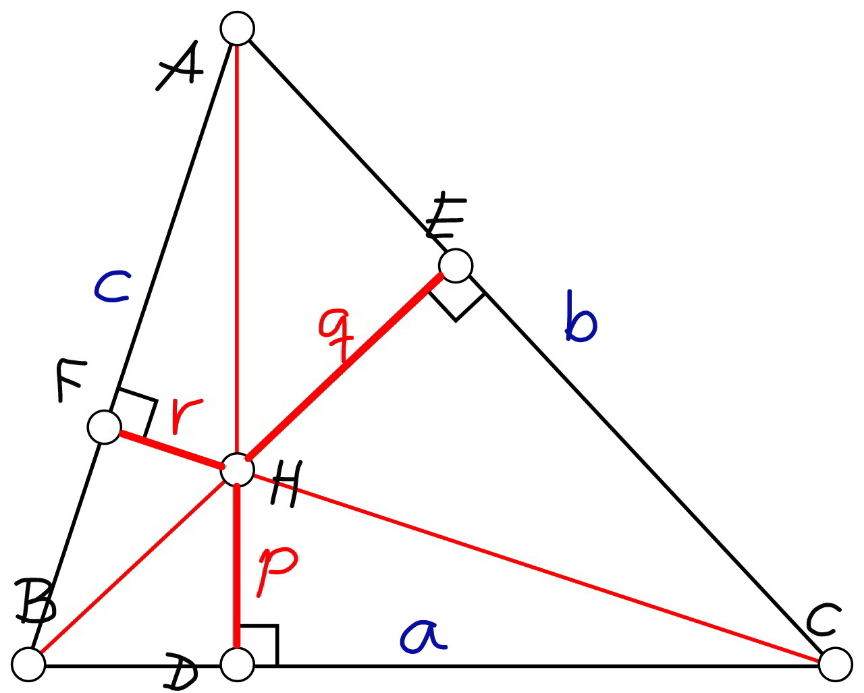
Commented by mr W last updated on 24/Dec/21

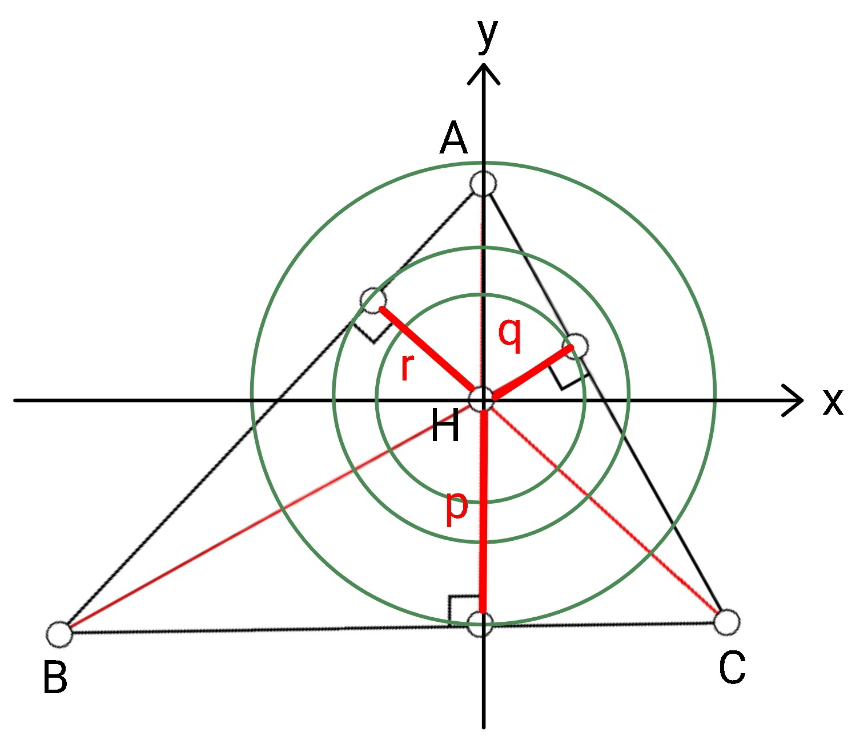
Commented by mr W last updated on 24/Dec/21

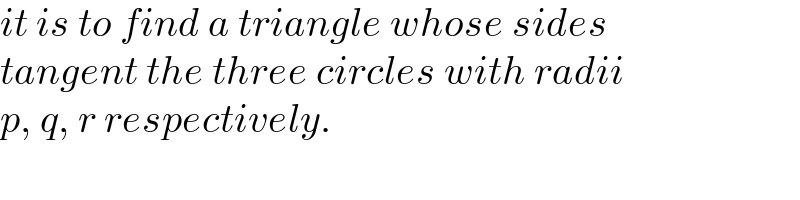
$i t i s t o f i n d a t r i a n g l e w h o s e s i d e s$ $t a n g e n t t h e t h r e e c i r c l e s w i t h r a d i i$ $p, q, r r e s p e c t i v e l y .$
Commented by mr W last updated on 24/Dec/21

$i f t h e d i s t a n c e s f r o m t h e o r t h o c e n t e r$ $o f a t r i a n g l e t o i t s s i d e s a r e p, q, r$ $r e s p e c t i v e l y, f i n d t h e s i d e l e n g t h e s$ $o f t h e t r i a n g l e .$
Commented by henderson last updated on 24/Dec/21

$very interesting . . .$ $i want to know it!$
Commented by mr W last updated on 25/Dec/21

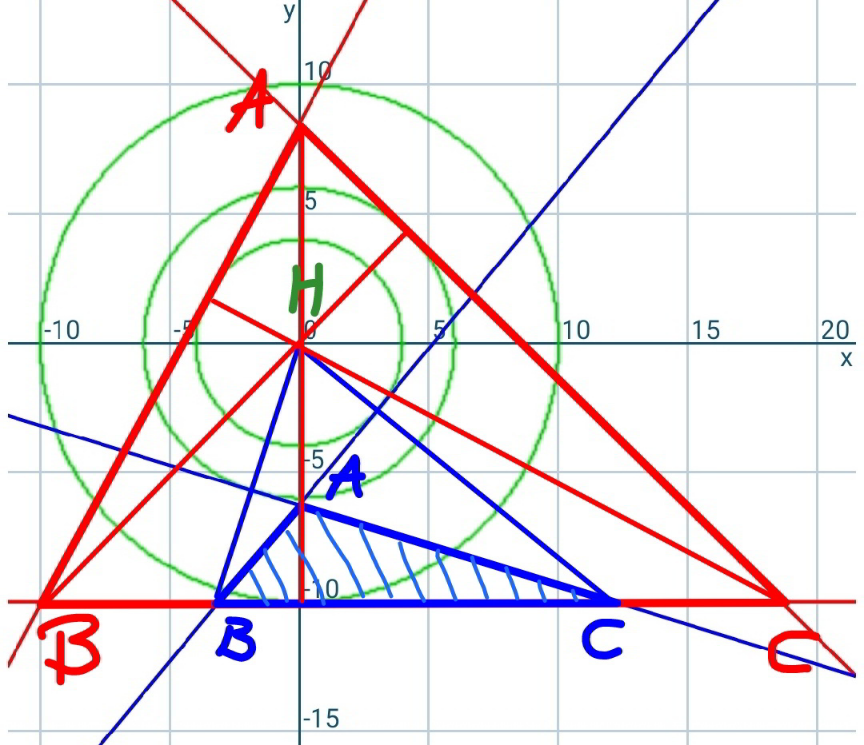
Commented by mr W last updated on 25/Dec/21

$g e n e r a l l y w e c a n f i n d t w o t r i a n g l e s$ $u n d e r t h e g i v e n c o n d i t i o n .$ $r e d t r i a n g l e w i t h o r t h o c e n t e r i n s i d e$ $b l u e t r i a n g l e w i t h o r t h o c e n t e r o u t s i d e$
	Answered by mr W last updated on 25/Dec/21

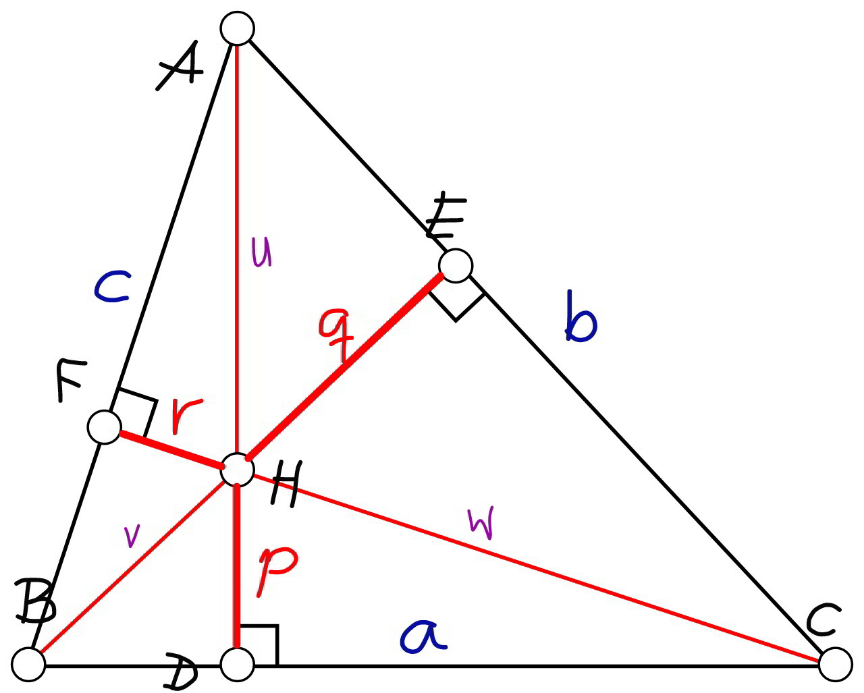
	Commented by mr W last updated on 26/Dec/21
	$(p/v)=(q/u) ⇒pu=qv (p/w)=(r/u) ⇒pu=rw ⇒ determinant (((pu=qv=rw)))=(1/k), say ⇒u=(1/(pk)), v=(1/(qk)), w=(1/(rk)) say the area of triangle ABC is Δ and the side lengthes are a, b, c. (1/2)a(p+u)=(1/2)b(q+v)=(1/2)c(r+w)=Δ (1/2)(au+bv+cw)=2Δ (1/2)(((2Δu)/(p+u))+((2Δv)/(q+v))+((2Δw)/(r+w)))=2Δ ⇒ determinant ((((u/(p+u))+(v/(q+v))+(w/(r+w))=2))) (1/((p/u)+1))+(1/((q/v)+1))+(1/((r/w)+1))=2 (1/(p^2 k+1))+(1/(q^2 k+1))+(1/(r^2 k+1))=2 (p^2 k+1)(q^2 k+1)+(q^2 k+1)(r^2 k+1)+(r^2 k+1)(p^2 k+1)=2(p^2 k+1)(q^2 k+1)(r^2 k+1) (p^2 q^2 +q^2 r^2 +r^2 p^2 )k^2 +2(p^2 +q^2 +r^2 )k+3=2p^2 q^2 r^2 k^3 +2(p^2 q^2 +q^2 r^2 +r^2 p^2 )k^2 +2(p^2 +q^2 +r^2 )k+2 2p^2 q^2 r^2 k^3 +(p^2 q^2 +q^2 r^2 +r^2 p^2 )k^2 −1=0 determinant ((((1/k^3 )−(p^2 q^2 +q^2 r^2 +r^2 p^2 ) (1/k)−2(pqr)^2 =0))) (pqr)^4 −(((p^2 q^2 +q^2 r^2 +r^2 p^2 )/3))^3 ≤0 ⇒three real roots (1/k_n )=2(√((p^2 q^2 +q^2 r^2 +r^2 p^2 )/3)) sin {((2nπ)/3)−(1/3) sin^(−1) [(pqr)^2 ((3/(p^2 q^2 +q^2 r^2 +r^2 p^2 )))^(3/2) ]} (n=0,1,2) generally two (i.e. n=1,2) of the three roots are suitable: determinant ((((1/k_1 )=2(√((p^2 q^2 +q^2 r^2 +r^2 p^2 )/3)) sin {(π/3)+(1/3) sin^(−1) [(pqr)^2 ((3/(p^2 q^2 +q^2 r^2 +r^2 p^2 )))^(3/2) ]})),(((1/k_2 )=−2(√((p^2 q^2 +q^2 r^2 +r^2 p^2 )/3)) sin {(π/3)−(1/3) sin^(−1) [(pqr)^2 ((3/(p^2 q^2 +q^2 r^2 +r^2 p^2 )))^(3/2) ]}))) the positive value is for the case that the orthocenter lies inside the triangle and the negative value for the case that it lies outside the triangle. with k we get 𝚫=(1/( (√(((1/(p+(1/(pk))))+(1/(q+(1/(qk))))+(1/(r+(1/(rk)))))(−(1/(p+(1/(pk))))+(1/(q+(1/(qk))))+(1/(r+(1/(rk)))))((1/(p+(1/(pk))))−(1/(q+(1/(qk))))+(1/(r+(1/(rk)))))((1/(p+(1/(pk))))+(1/(q+(1/(qk))))−(1/(r+(1/(rk))))))))) a=((2𝚫)/(p+(1/(pk)))), b=((2𝚫)/(q+(1/(qk)))), c=((2𝚫)/(r+(1/(rk)))) example: p=10, q=6, r=4 a≈28.522248 or 15.173152 b≈26.202978 or 12.655577 c≈20.945175 or 4.829686$
	$\frac{p}{v} = \frac{q}{u} \Rightarrow p u = q v$ $\frac{p}{w} = \frac{r}{u} \Rightarrow p u = r w$ $\Rightarrow \begin{matrix} p u = q v = r w \end{matrix} = \frac{1}{k}, s a y$ $\Rightarrow u = \frac{1}{p k}, v = \frac{1}{q k}, w = \frac{1}{r k}$ $s a y t h e a r e a o f t r i a n g l e A B C i s Δ$ $a n d t h e s i d e l e n g t h e s a r e a, b, c .$ $\frac{1}{2} a (p + u) = \frac{1}{2} b (q + v) = \frac{1}{2} c (r + w) = Δ$ $\frac{1}{2} (a u + b v + c w) = 2 Δ$ $\frac{1}{2} (\frac{2 Δ u}{p + u} + \frac{2 Δ v}{q + v} + \frac{2 Δ w}{r + w}) = 2 Δ$ $\Rightarrow \begin{matrix} \frac{u}{p + u} + \frac{v}{q + v} + \frac{w}{r + w} = 2 \end{matrix}$ $\frac{1}{\frac{p}{u} + 1} + \frac{1}{\frac{q}{v} + 1} + \frac{1}{\frac{r}{w} + 1} = 2$ $\frac{1}{p^{2} k + 1} + \frac{1}{q^{2} k + 1} + \frac{1}{r^{2} k + 1} = 2$ $(p^{2} k + 1) (q^{2} k + 1) + (q^{2} k + 1) (r^{2} k + 1) + (r^{2} k + 1) (p^{2} k + 1) = 2 (p^{2} k + 1) (q^{2} k + 1) (r^{2} k + 1)$ $(p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}) k^{2} + 2 (p^{2} + q^{2} + r^{2}) k + 3 = 2 p^{2} q^{2} r^{2} k^{3} + 2 (p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}) k^{2} + 2 (p^{2} + q^{2} + r^{2}) k + 2$ $2 p^{2} q^{2} r^{2} k^{3} + (p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}) k^{2} - 1 = 0$ $\begin{matrix} \frac{1}{k^{3}} - (p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}) \frac{1}{k} - 2 {(p q r)}^{2} = 0 \end{matrix}$ ${(p q r)}^{4} - {(\frac{p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}}{3})}^{3} ⩽ 0 \Rightarrow t h r e e r e a l r o o t s$ $\frac{1}{k_{n}} = 2 \sqrt{\frac{p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}}{3}} \sin {\frac{2 n π}{3} - \frac{1}{3} \sin^{- 1} [{(p q r)}^{2} {(\frac{3}{p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}})}^{\frac{3}{2}}]} (n = 0, 1, 2)$ $g e n e r a l l y t w o (i . e . n = 1, 2) o f t h e t h r e e$ $r o o t s a r e s u i t a b l e :$ $\begin{array}{cc} \frac{1}{k_{1}} = 2 \sqrt{\frac{p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}}{3}} \sin {\frac{π}{3} + \frac{1}{3} \sin^{- 1} [{(p q r)}^{2} {(\frac{3}{p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}})}^{\frac{3}{2}}]} \\ \frac{1}{k_{2}} = - 2 \sqrt{\frac{p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}}{3}} \sin {\frac{π}{3} - \frac{1}{3} \sin^{- 1} [{(p q r)}^{2} {(\frac{3}{p^{2} q^{2} + q^{2} r^{2} + r^{2} p^{2}})}^{\frac{3}{2}}]} \end{array}$ $t h e p o s i t i v e v a l u e i s f o r t h e c a s e t h a t$ $t h e o r t h o c e n t e r l i e s i n s i d e t h e t r i a n g l e$ $a n d t h e n e g a t i v e v a l u e f o r t h e c a s e$ $t h a t i t l i e s o u t s i d e t h e t r i a n g l e .$ $w i t h k w e g e t$ $Δ = \frac{1}{\sqrt{(\frac{1}{p + \frac{1}{p k}} + \frac{1}{q + \frac{1}{q k}} + \frac{1}{r + \frac{1}{r k}}) (- \frac{1}{p + \frac{1}{p k}} + \frac{1}{q + \frac{1}{q k}} + \frac{1}{r + \frac{1}{r k}}) (\frac{1}{p + \frac{1}{p k}} - \frac{1}{q + \frac{1}{q k}} + \frac{1}{r + \frac{1}{r k}}) (\frac{1}{p + \frac{1}{p k}} + \frac{1}{q + \frac{1}{q k}} - \frac{1}{r + \frac{1}{r k}})}}$ $a = \frac{2 Δ}{p + \frac{1}{p k}}, b = \frac{2 Δ}{q + \frac{1}{q k}}, c = \frac{2 Δ}{r + \frac{1}{r k}}$ $\underset{―}{e x a m p l e : p = 10, q = 6, r = 4}$ $a \approx 28.522248 o r 15.173152$ $b \approx 26.202978 o r 12.655577$ $c \approx 20.945175 o r 4.829686$
	Commented by mr W last updated on 25/Dec/21

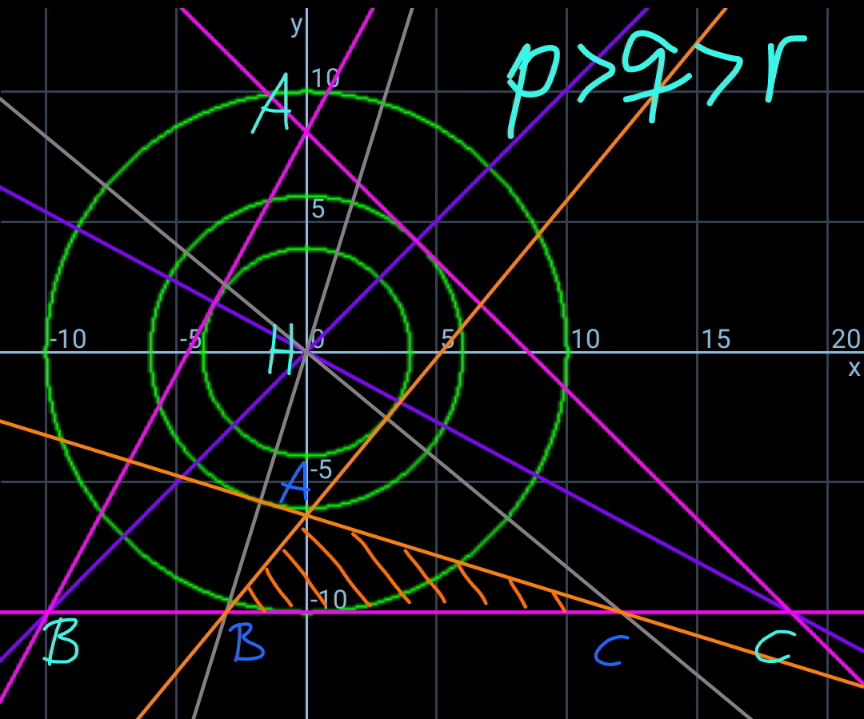
	Commented by mr W last updated on 25/Dec/21

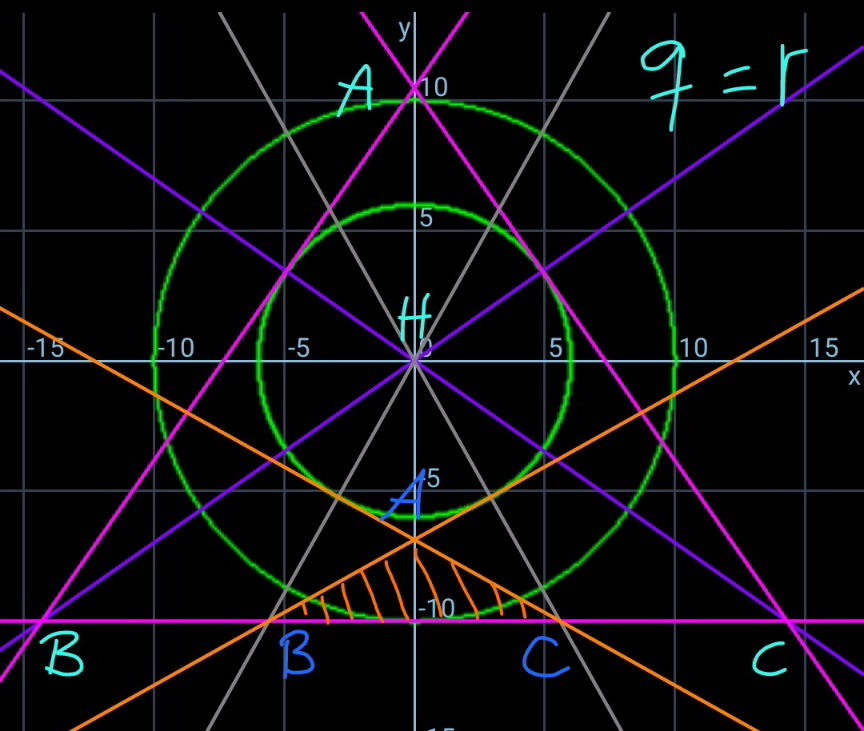
	Commented by mr W last updated on 25/Dec/21

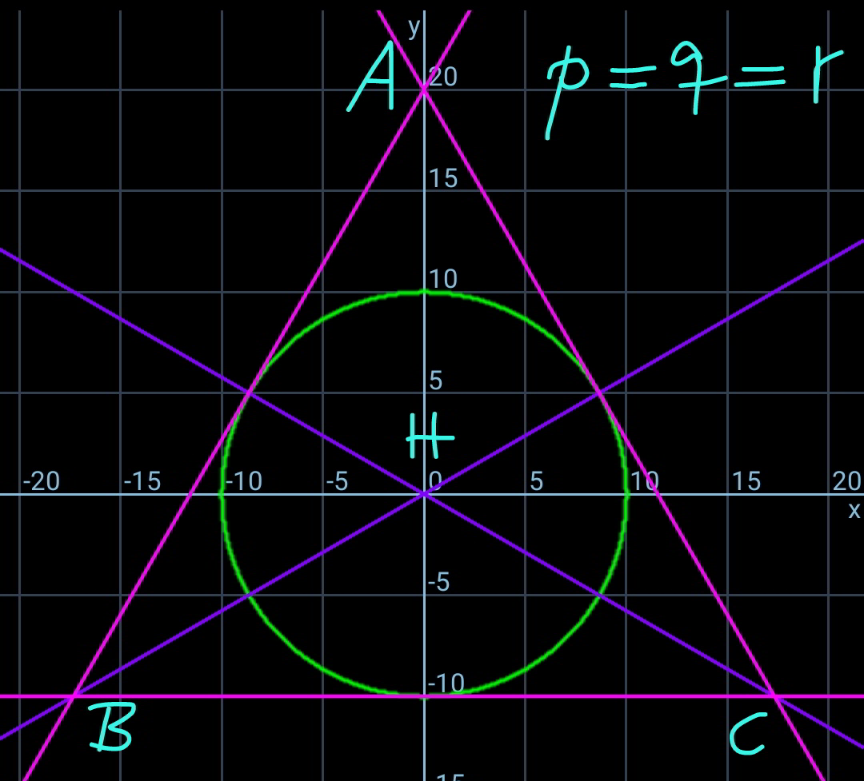
	Commented by Ar Brandon last updated on 25/Dec/21

	${What}^{'} s all this, Sir$ 🙁☹️
	Commented by mr W last updated on 25/Dec/21

	$h o w t o f i n d t h e t r i a n g l e i f y o u o n l y$ $k n o w t h e d i s t a n c e s f r o m i t s$ $o r t h o c e n t e r t o i t s t h r e e s i d e s .$
	Commented by Ar Brandon last updated on 25/Dec/21

	😭
	Commented by Tawa11 last updated on 25/Dec/21

	$Wow, great sir .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum