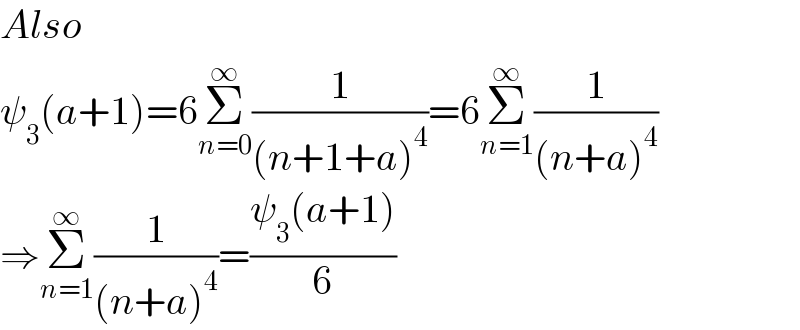Question and Answers Forum
Question Number 162368 by mr W last updated on 29/Dec/21
Commented by mr W last updated on 29/Dec/21
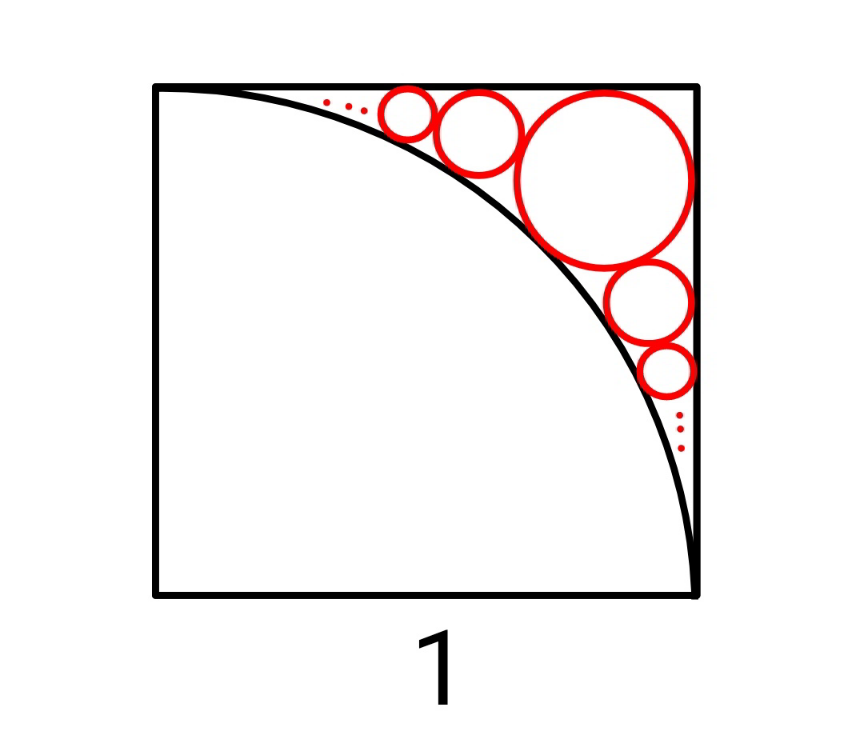
Commented by mr W last updated on 29/Dec/21
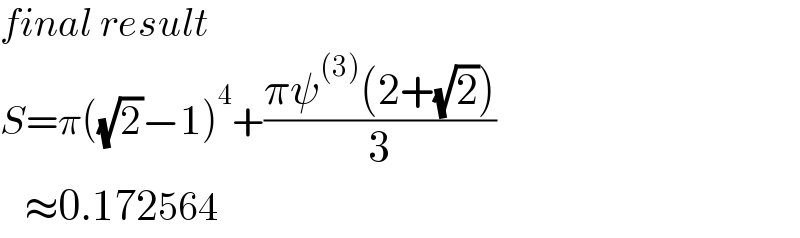
Answered by aleks041103 last updated on 29/Dec/21
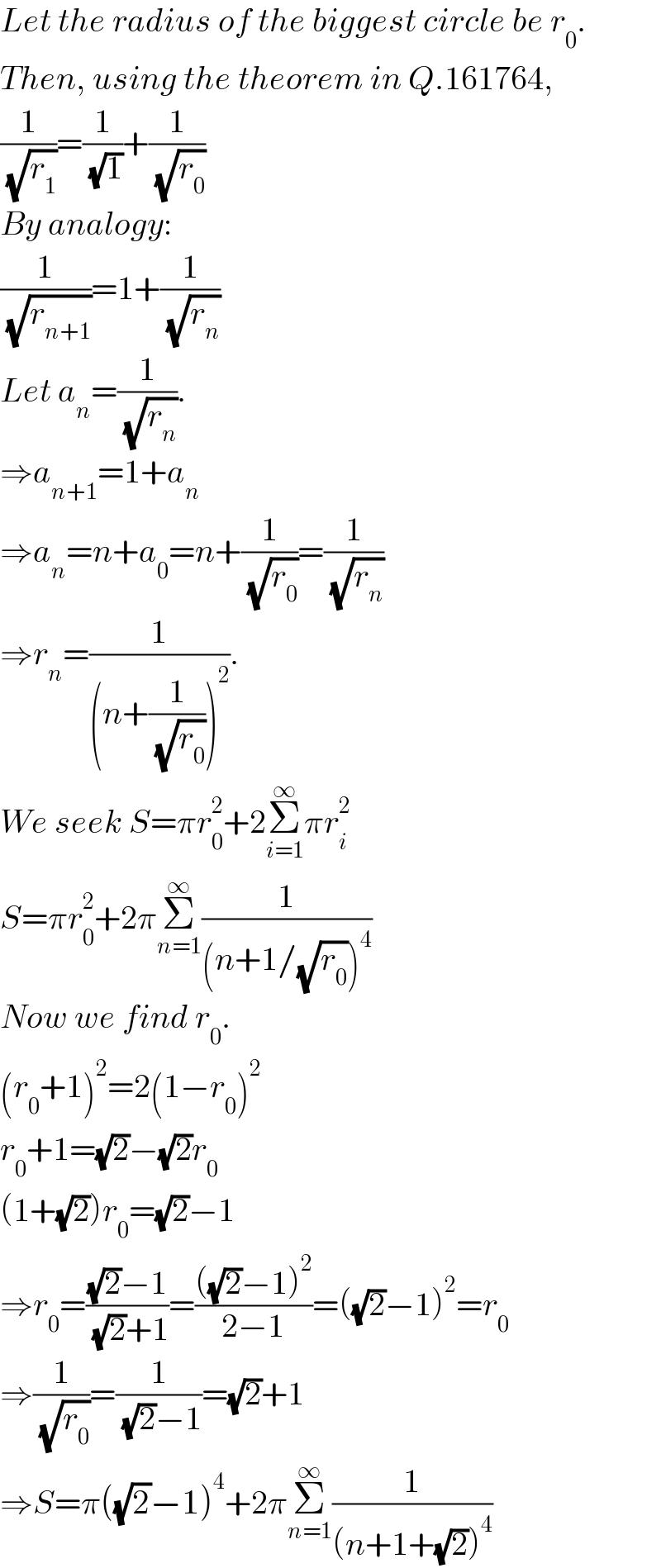
Commented by mr W last updated on 29/Dec/21
Commented by mr W last updated on 29/Dec/21
Commented by aleks041103 last updated on 29/Dec/21

Commented by aleks041103 last updated on 29/Dec/21

Commented by mr W last updated on 29/Dec/21
Commented by aleks041103 last updated on 29/Dec/21