
Question and Answers Forum
Question Number 16277 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

Answered by mrW1 last updated on 20/Jun/17
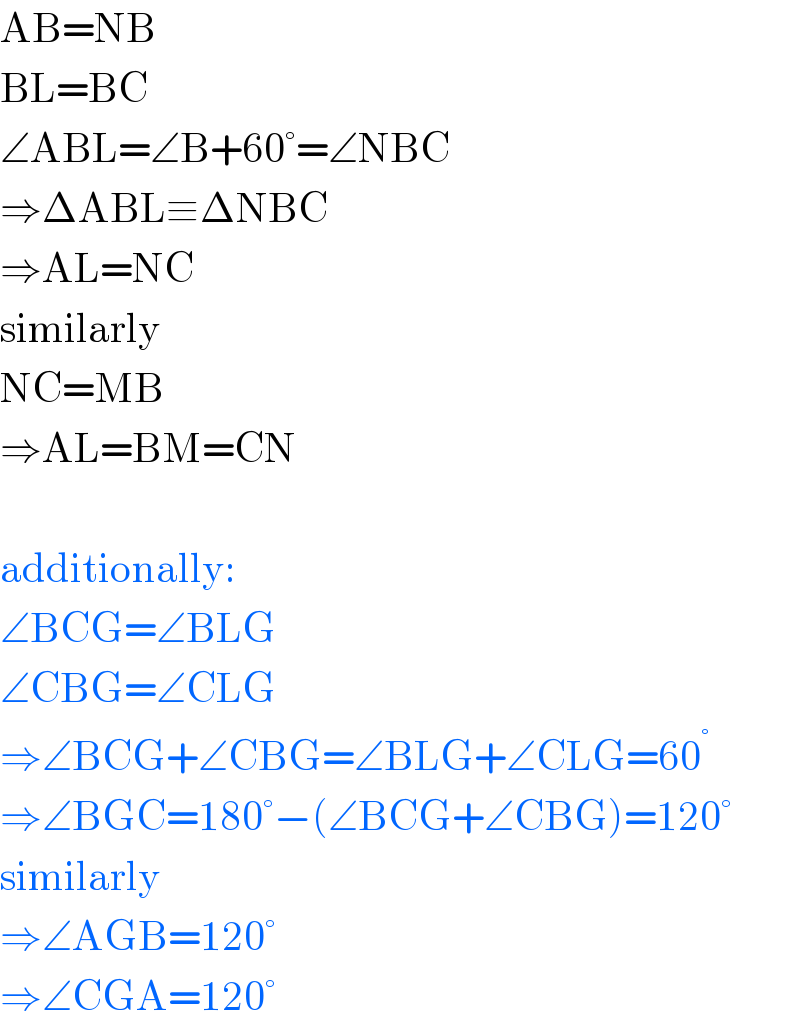
Commented by ajfour last updated on 20/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17
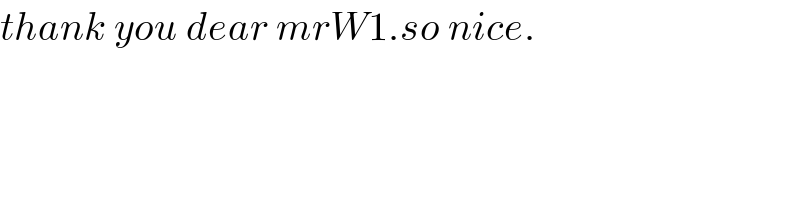
Answered by ajfour last updated on 20/Jun/17
![In ΔNAC CN^( 2) =b^2 +c^2 −2bccos (A+π/3) In ΔMCB BM^( 2) =a^2 +b^2 −2abcos (C+π/3) CN^( 2) −BM^( 2) = c^2 −a^2 −2b[ccos (A+π/3)−acos (C+π/3)] =c^2 −a^2 −2b{((ccos A)/2)−((c(√3)sin A)/2) −((acos C)/2)+((a(√3))/2)sin C } =c^2 −a^2 −b[ccos A−acos C] =c^2 −a^2 −b[((c(b^2 +c^2 −a^2 ))/(2bc))−((a(a^2 +b^2 −c^2 ))/(2ab))] =c^2 −a^2 −(1/2)[b^2 +c^2 −a^2 −a^2 −b^2 +c^2 ] = c^2 −a^2 −(c^2 −a^2 ) =0 Hence CN=BM similarly CN^( 2) −AL^2 =0 can be proved . ⇒ AL = BM = CN .](Q16282.png)
Commented by ajfour last updated on 20/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17
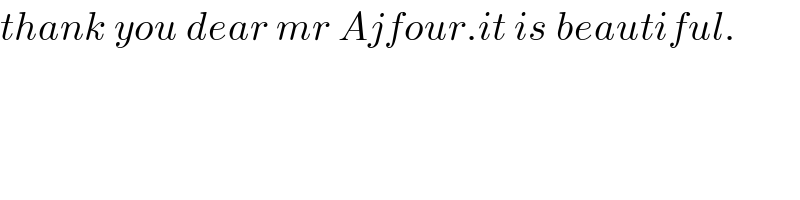
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

