
Question and Answers Forum
Question Number 163662 by amin96 last updated on 09/Jan/22
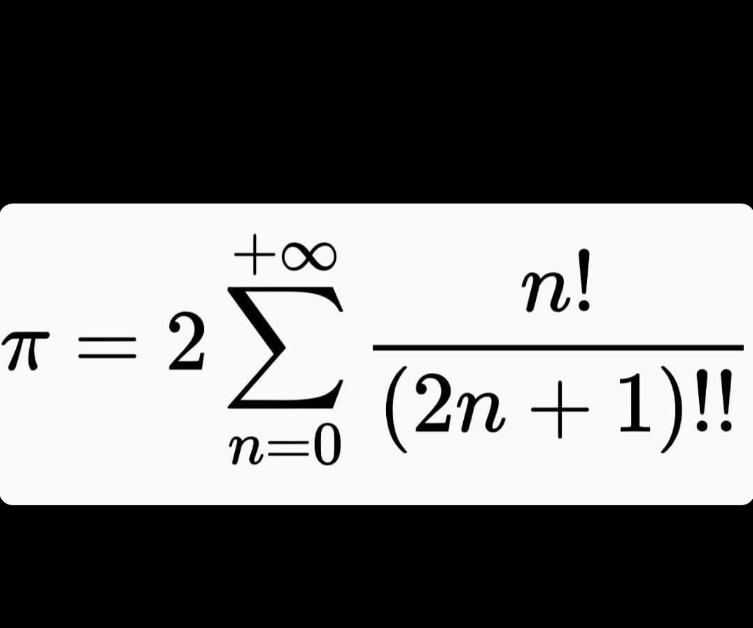
Commented by amin96 last updated on 09/Jan/22

Answered by Ar Brandon last updated on 09/Jan/22
![S=2Σ_(n=0) ^∞ ((n!)/((2n+1)!!))=2Σ_(n=0) ^∞ ((n!×n!×2^n )/((2n+1)!))=Σ_(n=0) ^∞ ((Γ^2 (n+1))/(Γ(2n+2)))×2^(n+1) =Σ_(n=0) ^∞ 2^(n+1) β(n+1, n+1)=Σ_(n=0) ^∞ 2^(n+1) ∫_0 ^1 x^n (1−x)^n dx =2∫_0 ^1 Σ_(n=0) ^∞ (2x−2x^2 )^n dx=2∫_0 ^1 (dx/(2x^2 −2x+1)) =∫_0 ^1 (dx/((x−(1/2))^2 +(1/4)))=2[arctan(2x−1)]_0 ^1 =2((π/4)+(π/4))=2×(π/2)=π](Q163694.png)
Commented by amin96 last updated on 09/Jan/22

| ||
Question and Answers Forum | ||
Question Number 163662 by amin96 last updated on 09/Jan/22 | ||
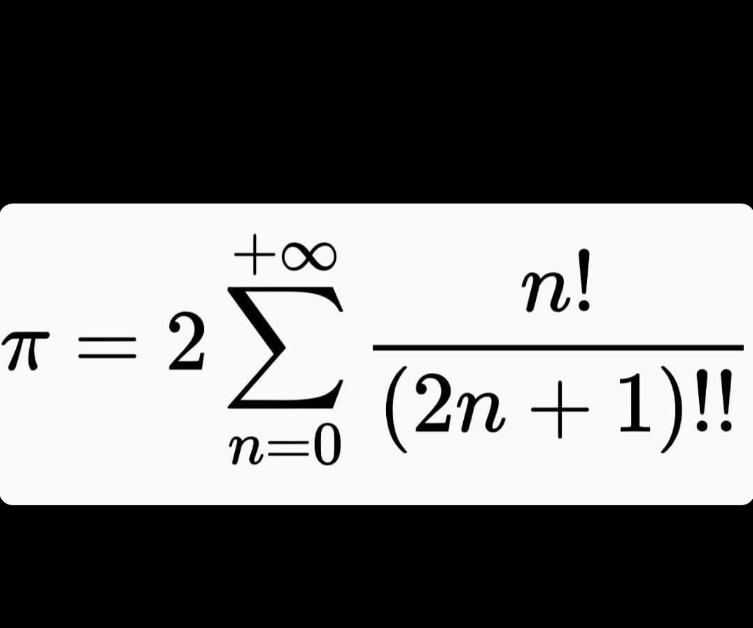 | ||
Commented by amin96 last updated on 09/Jan/22 | ||
 | ||
Answered by Ar Brandon last updated on 09/Jan/22 | ||
![S=2Σ_(n=0) ^∞ ((n!)/((2n+1)!!))=2Σ_(n=0) ^∞ ((n!×n!×2^n )/((2n+1)!))=Σ_(n=0) ^∞ ((Γ^2 (n+1))/(Γ(2n+2)))×2^(n+1) =Σ_(n=0) ^∞ 2^(n+1) β(n+1, n+1)=Σ_(n=0) ^∞ 2^(n+1) ∫_0 ^1 x^n (1−x)^n dx =2∫_0 ^1 Σ_(n=0) ^∞ (2x−2x^2 )^n dx=2∫_0 ^1 (dx/(2x^2 −2x+1)) =∫_0 ^1 (dx/((x−(1/2))^2 +(1/4)))=2[arctan(2x−1)]_0 ^1 =2((π/4)+(π/4))=2×(π/2)=π](Q163694.png) | ||
| ||
Commented by amin96 last updated on 09/Jan/22 | ||
 | ||