Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 16595 by ajfour last updated on 24/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/Jun/17

$y o u a r e w e l l c o m e d e a r m r A j f o u r . p l e a s e$ $p o s t y o u r a n s w e r . i a m w a i t i n g f o r i t .$
Commented by ajfour last updated on 24/Jun/17

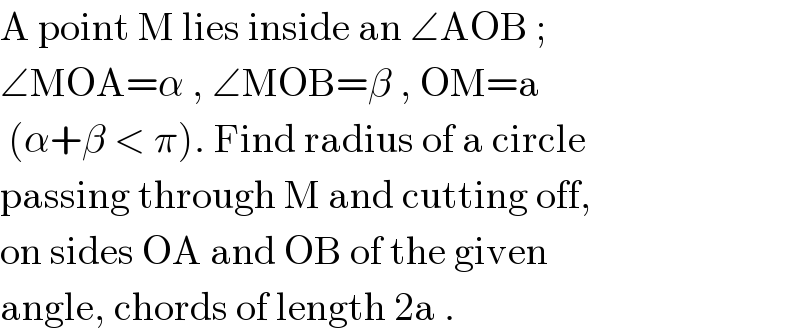
$A point M lies inside an ∠ AOB;$ $∠ MOA = α, ∠ MOB = β, OM = a$ $(α + β < π) . Find radius of a circle$ $passing through M and cutting off,$ $on sides OA and OB of the given$ $angle, chords of length 2 a .$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 26/Jun/17

$o C = x, o D = y,^{'} P^{'} c e n t e r o f c i r c l e . α + β = φ$ $C, i s t h e i n t e r s e c t o f o B w i t h c i r c l e .$ $D, i s t h e i n t e r s e c t o f o A w i t h c i r c l e .$ $N, i s t h e i n t e r s e c t o f o M w i t h c i r c l e$ $w h e n c o n t i n u e d .$ ${o p}^{2} - R^{2} = o D . o A = y (2 a + y)$ ${o p}^{2} - R^{2} = o C . o . B = x (2 a + x)$ $\Rightarrow y (2 a + y) = x (2 a + x) \Rightarrow x^{2} - y^{2} + 2 a (x - y) = 0$ $\Rightarrow (x - y) (x + y + 2 a) = 0 \Rightarrow x = y = o C = o D .$ ${C D}^{2} = 2 x^{2} - 2 x^{2} c o s φ = 4 x^{2} {s i n}^{2} \frac{φ}{2} \Rightarrow$ $C D = 2 x . s i n \frac{φ}{2}$ ${A B}^{2} = {(x + 2 a)}^{2} + {(y + 2 a)}^{2} - 2 (x + 2 a) (y + 2 a) c o s φ u \Rightarrow$ $A B = 2 (x + 2 a) s i n \frac{φ}{2}$ ${B D}^{2} = x^{2} + {(x + 2 a)}^{2} - 2 x (x + 2 a) c o s φ =$ $= 2 x^{2} + 4 a^{2} + 4 a x - 2 x^{2} c o s φ - 4 a x c o s φ =$ $= 2 (x^{2} - 2 a x) (1 - c o s φ) + 4 a^{2} =$ $= 4 (x^{2} + 2 a x) {s i n}^{2} \frac{φ}{2} + 4 a^{2}$ $\Rightarrow B D = 2 \sqrt{a^{2} + (x^{2} + 2 a x) {s i n}^{2} \frac{φ}{2}}$ $C A = 2 \sqrt{a^{2} + (x^{2} + 2 a x) {s i n}^{2} \frac{φ}{2}}$ ${D M}^{2} = a^{2} + x^{2} - 2 a x c o s α$ ${C M}^{2} = a^{2} + x^{2} - 2 a x c o s β$ ${A M}^{2} = a^{2} + {(2 a + x)}^{2} - 2 x (2 a + x) c o s α$ $(x + 2 a) ({D M}^{2} + 2 a x) = 2 a . a^{2} + x . {A M}^{2}$ $(x + 2 a) (a^{2} + x^{2} - 2 a x c o s α + 2 a x) = 2 a^{3} + x [a^{2} + {(2 a + x)}^{2} - 2 x (2 a + x) c o s α] \Rightarrow$ ${x a}^{2} + x^{3} - 2 {a x}^{2} c o s α + 2 {a x}^{2} + 2 a^{3} + 2 {a x}^{2} - 4 a^{2} x c o s α + 4 a^{2} x =$ $= 2 a^{3} + {x a}^{2} + x {(2 a + x)}^{2} - 2 x^{2} (2 a + x) c o s α$ $\Rightarrow - 2 {a x}^{2} c o s α - 2 x^{3} c o s α + 4 a^{2} x c o s α = 0$ $\Rightarrow x^{2} + a x - 2 a^{2} = 0 \Rightarrow x = \frac{- a \pm \sqrt{a^{2} + 8 a^{2}}}{2}$ $\Rightarrow x = y = \frac{- a + 3 a}{2} = a$ $C D = 2 a s i n \frac{φ}{2}, A B = 6 a s i n \frac{φ}{2},$ $B D = C A = 2 a \sqrt{1 + 3 {s i n}^{2} \frac{φ}{2}}$ $D M = 2 a s i n \frac{α}{2}, C M = 2 a s i n \frac{β}{2}$ $a^{2} = a^{2} + {D M}^{2} - 2 a . D M . c o s (o D M)$ $\Rightarrow c o s (o D M) = \frac{D M}{2 a} = \frac{2 a s i n \frac{α}{2}}{2 a} = s i n \frac{α}{2}$ $\Rightarrow o D M = \frac{π}{2} - \frac{α}{2}$ ${M B}^{2} = {M D}^{2} + {B D}^{2} - 2 M D . B D . c o s (M D B)$ ${M B}^{2} = a^{2} + 9 a^{2} - 6 a^{2} c o s β = 2 a^{2} (5 - 3 c o s β)$ $10 a^{2} - 6 a^{2} c o s β = 4 a^{2} {s i n}^{2} \frac{α}{2} + 4 a^{2} (1 + 3 {s i n}^{2} \frac{φ}{2}) - 8 a^{2} s i n \frac{α}{2} \sqrt{1 + 3 {s i n}^{2} \frac{φ}{2}} . c o s (M D B)$ $2 a^{2} - 6 a^{2} c o s β + 2 a^{2} c o s α - 6 a^{2} c o s (α + β) = - 8 a^{2} s i n \frac{α}{2} \sqrt{1 + 3 {s i n}^{2} \frac{α + β}{2}} . c o s (M D B)$ $\overset{}{\Rightarrow} c o s (M D B) = \sqrt{2} . \frac{3 c o s (α + β) + 3 c o s β - c o s α - 1}{2 s i n \frac{α}{2} . \sqrt{5 - 3 c o s (α + β)}}$
Commented by ajfour last updated on 25/Jun/17

$huge will and effort Sir, should$ $i mention the answer ?$
	Answered by ajfour last updated on 25/Jun/17

	$R = a \sqrt{1 + 4 \frac{\cos^{2} (\frac{α - β}{2}) \sin^{2} (\frac{α + β}{2})}{\cos^{4} (\frac{α + β}{2})}}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum