
Question and Answers Forum
Question Number 167267 by mnjuly1970 last updated on 11/Mar/22
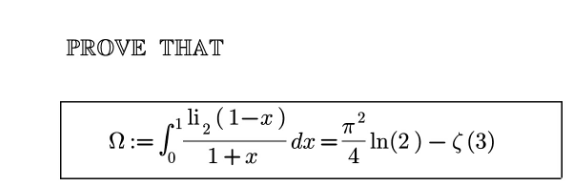
Answered by mindispower last updated on 15/Mar/22
![IBP⇒Ω=[ln(1+x)Li_2 (1−x)]_0 ^1 −∫_0 ^1 ((ln(1+x)ln(x))/(1−x))dx =−∫_0 ^1 ((ln(x)ln(1+x))/(1−x))dx ln(1+x)=Σ_(j≥0) (((−1)^j )/(j+1))x^(j+1) (1/(1−x))=Σ_(k≥0) x^k ((ln(1+x))/(1−x))=Σ_(n≥0) Σ_(m=0) ^n (((−1)^m )/(m+1))x^(n+1) =S Σ_(m=0) ^n (((−1)^m )/(m+1))=−H_(n+1) ^− S=−Σ_(n≥0) H_(n+1) ^− x^(n+1) =−Σ_(n≥1) H_n x^n Ω=−Σ_(n≥1) ∫_0 ^1 H_n ^− x^n ln(x)dx =Σ_(n≥1) (H_n ^− /((n+1)^2 ))=Σ_(n≥1) ((H_(n+1) ^− +(((−1)^n )/(n+1)))/((n+1)^2 )) =Σ_(n≥1) (H_(n+1) ^− /((n+1)^2 ))+Σ_(n≥1) (((−1)^n )/((n+1)^3 )) =Σ_(n≥1) (H_n ^− /n^2 )−η(3)=Ω Σ_(n≥1) (H_n ^− /n^(q+1) )=ζ(q)ln(2)−(q/2)ζ(q+1)+η(q+1)+Σ_(k=1) ^q η(k)η(q+1−k) Euler formula For harominc sum Ω=ζ(2)ln(2)−ζ(3)+η(3)+η(1)η(2)−η(3) =ζ(2)ln(2)−ζ(3)+(1/2)ln(2)ζ(2) =(3/2_ )ln(2).(π^2 /6)−ζ(3) =(π^2 /4)ln(2)−ζ(3)](Q167397.png)
| ||
Question and Answers Forum | ||
Question Number 167267 by mnjuly1970 last updated on 11/Mar/22 | ||
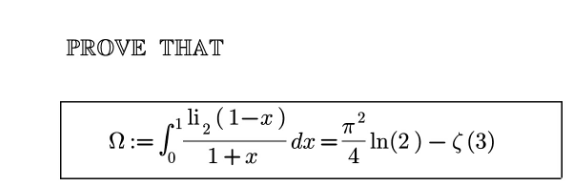 | ||
Answered by mindispower last updated on 15/Mar/22 | ||
![IBP⇒Ω=[ln(1+x)Li_2 (1−x)]_0 ^1 −∫_0 ^1 ((ln(1+x)ln(x))/(1−x))dx =−∫_0 ^1 ((ln(x)ln(1+x))/(1−x))dx ln(1+x)=Σ_(j≥0) (((−1)^j )/(j+1))x^(j+1) (1/(1−x))=Σ_(k≥0) x^k ((ln(1+x))/(1−x))=Σ_(n≥0) Σ_(m=0) ^n (((−1)^m )/(m+1))x^(n+1) =S Σ_(m=0) ^n (((−1)^m )/(m+1))=−H_(n+1) ^− S=−Σ_(n≥0) H_(n+1) ^− x^(n+1) =−Σ_(n≥1) H_n x^n Ω=−Σ_(n≥1) ∫_0 ^1 H_n ^− x^n ln(x)dx =Σ_(n≥1) (H_n ^− /((n+1)^2 ))=Σ_(n≥1) ((H_(n+1) ^− +(((−1)^n )/(n+1)))/((n+1)^2 )) =Σ_(n≥1) (H_(n+1) ^− /((n+1)^2 ))+Σ_(n≥1) (((−1)^n )/((n+1)^3 )) =Σ_(n≥1) (H_n ^− /n^2 )−η(3)=Ω Σ_(n≥1) (H_n ^− /n^(q+1) )=ζ(q)ln(2)−(q/2)ζ(q+1)+η(q+1)+Σ_(k=1) ^q η(k)η(q+1−k) Euler formula For harominc sum Ω=ζ(2)ln(2)−ζ(3)+η(3)+η(1)η(2)−η(3) =ζ(2)ln(2)−ζ(3)+(1/2)ln(2)ζ(2) =(3/2_ )ln(2).(π^2 /6)−ζ(3) =(π^2 /4)ln(2)−ζ(3)](Q167397.png) | ||
| ||