Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 168499 by infinityaction last updated on 12/Apr/22

Answered by MJS_new last updated on 12/Apr/22

$$\left(1\right)t=\tan \frac{x}{2}$$$$\left(2\right)u=\frac{\sqrt{1-t}}{\sqrt{1+t}}$$$$\Rightarrow$$$$-\int (u^{10}+u^6)du$$$$\mathrm{sorry}{\mathrm{I}}^{\prime }\mathrm{m}\mathrm{too}\mathrm{lazy}\mathrm{to}\mathrm{write}\mathrm{it}\mathrm{all}\mathrm{down}.$$

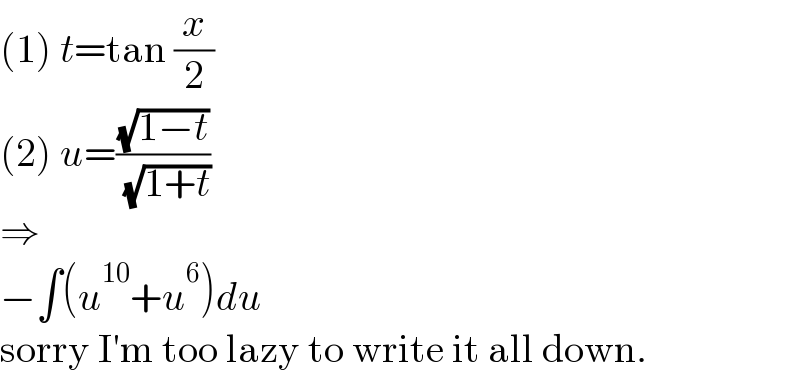
Commented by infinityaction last updated on 12/Apr/22

$$sirpleaseexplainalittlemore$$

Answered by MJS_new last updated on 12/Apr/22

$$\mathrm{easier}:$$$$\int \frac{{\sec }^{2}x}{{(\sec x+\tan x)}^{9/2}}dx=$$$$[t=\sin x\to dx=\frac{dt}{\cos x}]$$$$=\int \frac{{(1-t)}^{3/4}}{{(1+t)}^{15/4}}dt=$$$$[u=\frac{{(1-t)}^{1/4}}{{(1+t)}^{1/4}}\to dt=-2{(1-t)}^{3/4}{(1+t)}^{5/4}du]$$$$=-\int u^{10}+u^{6}du=-\frac{u^{11}}{11}-\frac{u^7}{7}=$$$$=-\frac{2(9+2t){(1-t)}^{7/4}}{77{(1+t)}^{11/4}}=$$$$=-\frac{2(9+2\sin x){(1-\sin x)}^{7/4}}{77{(1+\sin x)}^{11/4}}+C$$

Commented by peter frank last updated on 13/Apr/22

$$\mathrm{thank}\mathrm{you}$$

Commented by infinityaction last updated on 13/Apr/22

$$thankyousir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com