
Question and Answers Forum
Question Number 168857 by Sotoberry last updated on 19/Apr/22
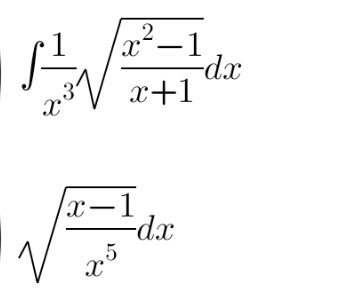
Answered by MJS_new last updated on 20/Apr/22
![∫(1/x^3 )(√((x^2 −1)/(x+1)))dx=∫((√(x−1))/x^3 )dx= [t=(√(x−1)) → dx=2(√(x−1))dt] =2∫(t^2 /((t^2 +1)^3 ))dt=((t(t^2 −1))/(4(t^2 +1)^2 ))+(1/4)arctan t = =(((x−2)(√(x−1)))/(4x^2 ))+(1/4)arctan (√(x−1)) +C](Q168870.png)
Answered by MJS_new last updated on 20/Apr/22
![∫(√((x−1)/x^5 ))dx= t=(√((x−1)/x)) → dx=2x^2 (√((x−1)/x))dt] =2∫t^2 dt=((2t^3 )/3)=(2/3)(√(((x−1)^3 )/x^3 ))+C](Q168871.png)
Answered by cortano1 last updated on 20/Apr/22
![∫ ((√(x−1))/( (√x^5 ))) dx= ∫ (((√(1−x^(−1) )) dx)/x^2 ) = ∫ x^(−2) (√(1−x^(−1) )) dx [ let u^2 =1−x^(−1) ⇒2u du = x^(−2) dx ] I= ∫ u (2u du)= (2/3)u^3 +c = (2/3) (((x−1)/x))(√((x−1)/x)) + c](Q168893.png)
| ||
Question and Answers Forum | ||
Question Number 168857 by Sotoberry last updated on 19/Apr/22 | ||
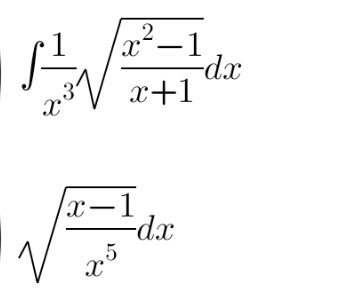 | ||
Answered by MJS_new last updated on 20/Apr/22 | ||
![∫(1/x^3 )(√((x^2 −1)/(x+1)))dx=∫((√(x−1))/x^3 )dx= [t=(√(x−1)) → dx=2(√(x−1))dt] =2∫(t^2 /((t^2 +1)^3 ))dt=((t(t^2 −1))/(4(t^2 +1)^2 ))+(1/4)arctan t = =(((x−2)(√(x−1)))/(4x^2 ))+(1/4)arctan (√(x−1)) +C](Q168870.png) | ||
| ||
Answered by MJS_new last updated on 20/Apr/22 | ||
![∫(√((x−1)/x^5 ))dx= t=(√((x−1)/x)) → dx=2x^2 (√((x−1)/x))dt] =2∫t^2 dt=((2t^3 )/3)=(2/3)(√(((x−1)^3 )/x^3 ))+C](Q168871.png) | ||
| ||
Answered by cortano1 last updated on 20/Apr/22 | ||
![∫ ((√(x−1))/( (√x^5 ))) dx= ∫ (((√(1−x^(−1) )) dx)/x^2 ) = ∫ x^(−2) (√(1−x^(−1) )) dx [ let u^2 =1−x^(−1) ⇒2u du = x^(−2) dx ] I= ∫ u (2u du)= (2/3)u^3 +c = (2/3) (((x−1)/x))(√((x−1)/x)) + c](Q168893.png) | ||
| ||