Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 168926 by mr W last updated on 22/Apr/22

Commented by mr W last updated on 22/Apr/22

$$M=midpointofAa$$$$L=midpointofBb$$$$K=midpointofCc$$$$prove$$$$1.{\mathrm{\Delta }}_{abc}=4{\mathrm{\Delta }}_{MLK}$$$$2.ab+bc+ca⩽2(ML+LK+KM)$$

Commented by mr W last updated on 22/Apr/22

$$relatedtoQ168606$$

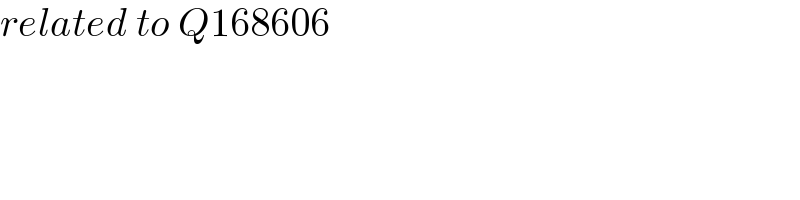
Answered by mr W last updated on 22/Apr/22

$$\underset{―}{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{I}}$$$$AH=\frac{Ac}{\sin B}=\frac{b\cos A}{\sin B}=\frac{2R\sin B\cos A}{\sin B}=2R\cos A$$$$similarly$$$$BH=2R\cos B$$$$CH=2R\cos C$$$$$$$$Ha=\frac{Ba}{\tan C}=\frac{c\cos B}{\tan C}=\frac{2R\sin C\cos B}{\tan C}=2R\cos B\cos C$$$$similarly$$$$Hb=2R\cos C\cos A$$$$Hc=2R\cos A\cos B$$$$$$$$HM=AH-\frac{AH+Ha}{2}=\frac{1}{2}(AH-Ha)$$$$=R(\cos A-\cos B\cos C)$$$$HL=BH-\frac{BH+Hb}{2}=\frac{1}{2}(BH-Hb)$$$$=R(\cos B-\cos C\cos A)$$$$HK=CH-\frac{CH+Hc}{2}=\frac{1}{2}(CH-Hc)$$$$=R(\cos C-\cos A\cos B)$$$$$$$$2{\mathrm{\Delta }}_{abc}=HM\times HL\times \sin C+HL\times HK\times \sin A+HK\times HM\times \sin B$$$$2{\mathrm{\Delta }}_{abc}=4R^2(\cos B\cos C\times \cos C\cos A\times \sin C+\cos C\cos A\times \cos A\cos B\times \sin A+\cos A\cos B\times \cos B\cos C\times \sin B)$$$${\mathrm{\Delta }}_{abc}=R^2\cos A\cos B\cos C(\sin 2A+\sin 2B+\sin 2C)$$$${\mathrm{\Delta }}_{abc}=4R^2\cos A\cos B\cos C\sin A\sin B\sin C$$$$\Rightarrow {\mathrm{\Delta }}_{abc}=\frac{R^2}{2}\sin 2A\sin 2B\sin 2C$$$$$$$$2{\mathrm{\Delta }}_{MLK}=HM\times HL\times \sin C+HL\times HK\times \sin A+HK\times HM\times \sin B$$$$\frac{2}{R^2}{\mathrm{\Delta }}_{MLK}=(\cos A-\cos B\cos C)(\cos B-\cos C\cos A)\sin C+(\cos B-\cos C\cos A)(\cos C-\cos A\cos B)\sin A+(\cos C-\cos A\cos B)(\cos A-\cos B\cos C)\sin B$$$$\frac{2}{R^2}{\mathrm{\Delta }}_{MLK}=\cos A\cos B\cos C(\tan A+\tan B+\tan C)-\frac{1}{2}(\sin 2A+\sin 2B+\sin 2C)-\frac{1}{4}(\cos 2A\sin 2C+\cos 2B\sin 2C+\cos 2B\sin 2A+\cos 2C\sin 2A+\cos 2C\sin 2B+\cos 2A\sin 2B)+\frac{1}{2}\cos A\cos B\cos C(\sin 2A+\sin 2B+\sin 2C)$$$$\frac{2}{R^2}{\mathrm{\Delta }}_{MLK}=\cos A\cos B\cos C(\tan A+\tan B+\tan C)-\frac{1}{2}(\sin 2A+\sin 2B+\sin 2C)-\frac{1}{4}[\sin 2(A+C)+\sin 2(B+C)+\sin 2(A+B)]+\frac{1}{2}\cos A\cos B\cos C(\sin 2A+\sin 2B+\sin 2C)$$$$\frac{2}{R^2}{\mathrm{\Delta }}_{MLK}=\cos A\cos B\cos C\tan A\tan B\tan C-\frac{1}{2}(\sin 2A+\sin 2B+\sin 2C)+\frac{1}{4}(\sin 2A+\sin 2B+\sin 2C)+\frac{1}{2}\cos A\cos B\cos C(\sin 2A+\sin 2B+\sin 2C)$$$$\frac{2}{R^2}{\mathrm{\Delta }}_{MLK}=\sin A\sin B\sin C-\sin A\sin B\sin C+2\cos A\cos B\cos C\sin A\sin B\sin C$$$$\frac{2}{R^2}{\mathrm{\Delta }}_{MLK}=\frac{1}{4}\sin 2A\sin 2B\sin 2C$$$$\Rightarrow {\mathrm{\Delta }}_{MLK}=\frac{R^2}{8}\sin 2A\sin 2B\sin 2C$$$$\Rightarrow {\mathrm{\Delta }}_{abc}=4{\mathrm{\Delta }}_{MLK}$$

Commented by mr W last updated on 21/Apr/22

$$followingtheoremsareused:$$$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$$$\sin 2A+\sin 2B+\sin 2C=4\sin A\sin B\sin C$$$$\tan A+\tan B+\tan C=\tan A\tan B\tan C$$

Commented by Tawa11 last updated on 21/Apr/22

$$\mathrm{Great}\mathrm{sir}.$$

Answered by mr W last updated on 23/Apr/22

$$\underset{―}{\mathit{P}\mathit{a}\mathit{r}\mathit{t}\mathit{I}\mathit{I}}$$$$Ca=b\cos C=2R\cos B\cos C$$$$Cb=a\cos C=2R\cos A\cos C$$$${\left(ab\right)}^2={\left(2R\cos B\cos C\right)}^2+{\left(2R\cos A\cos C\right)}^2+2\times 2R\cos B\cos C\times 2R\cos A\cos C\times \cos C$$$$\frac{{\left(ab\right)}^2}{4R^2}=({\cos }^{2}A+{\cos }^{2}B+{\cos }^{2}C+2\cos A\cos B\cos C-{\cos }^{2}C){\cos }^{2}C$$$$\frac{{\left(ab\right)}^2}{4R^2}=(3-{\sin }^{2}A-{\sin }^{2}B-{\sin }^{2}C+2\cos A\cos B\cos C-{\cos }^{2}C){\cos }^{2}C$$$$\frac{{\left(ab\right)}^2}{4R^2}={\sin }^{2}C{\cos }^{2}C$$$$\Rightarrow ab=R\sin 2C$$$$ab+bc+ca=R(\sin 2A+\sin 2B+\sin 2C)$$$$\Rightarrow ab+bc+ca=4R\sin A\sin B\sin C$$$$$$$${LK}^2=R^2{(\cos B-\cos C\cos A)}^2+R^2{(\cos C-\cos A\cos B)}^2+2R^2(\cos B-\cos C\cos A)(\cos C-\cos A\cos B)\cos A$$$$\frac{{LK}^2}{R^2}={(\cos B-\cos C\cos A)}^2+{(\cos C-\cos A\cos B)}^2+2(\cos B-\cos C\cos A)(\cos C-\cos A\cos B)\cos A$$$$\frac{{LK}^2}{R^2}={\sin }^{2}A({\cos }^{2}B+{\cos }^{2}C-2\cos A\cos B\cos C)$$$$\frac{{LK}^2}{R^2}={\sin }^{2}A(3-{\sin }^{2}A-{\sin }^{2}B-{\sin }^{2}C-2\cos A\cos B\cos C-{\cos }^{2}A)$$$$\frac{{LK}^2}{R^2}={\sin }^{2}A(1-{\cos }^{2}A)$$$$\frac{{LK}^2}{R^2}={\sin }^{4}A$$$$\Rightarrow LK=R{\sin }^{2}A$$$$ML+LK+KM=R({\sin }^{2}A+{\sin }^{2}B+{\sin }^{2}C)$$$$⩾R\times 3\times {\left(\sin A\sin B\sin C\right)}^{\frac{2}{3}}$$$$>3R\sin A\sin B\sin C$$$$=\frac{3}{4}\times 4R\sin A\sin B\sin C$$$$=\frac{3}{4}(ab+bc+ca)$$$$\Rightarrow ab+bc+ca<\frac{4}{3}(ML+LK+KM)<2(ML+LK+KM)$$

Commented by Shrinava last updated on 23/Apr/22

$$\mathrm{PERFECT}\mathrm{DEAR}\mathrm{SIR}\mathrm{THANKS}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com