
Question and Answers Forum
Question Number 169559 by TOTTI last updated on 03/May/22
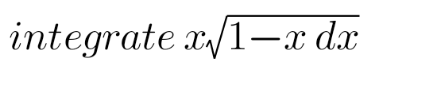
Commented by cortano1 last updated on 03/May/22
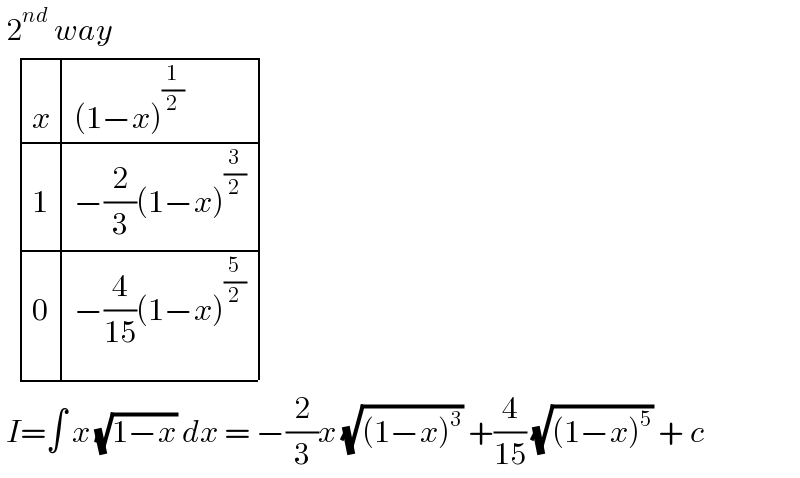
Answered by greougoury555 last updated on 03/May/22
![∫ x(√(1−x)) dx let (√(1−x)) = u → { ((x=1−u^2 )),((dx=−2u du)) :} I=∫ (1−u^2 )(u)(−2u)du =−2∫(1−u^2 )u^2 du =−2∫(u^2 −u^4 )du =−2[ (1/3)u^3 −(1/5)u^5 ]+c =−(2/(15))u^3 (5−3u^2 )+c =−(2/(15)) (√((1−x)^3 )) (5−3(1−x))+c =−(2/(15)) (3x+2)(√((1−x)^3 )) + c](Q169560.png)
| ||
Question and Answers Forum | ||
Question Number 169559 by TOTTI last updated on 03/May/22 | ||
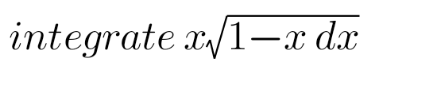 | ||
Commented by cortano1 last updated on 03/May/22 | ||
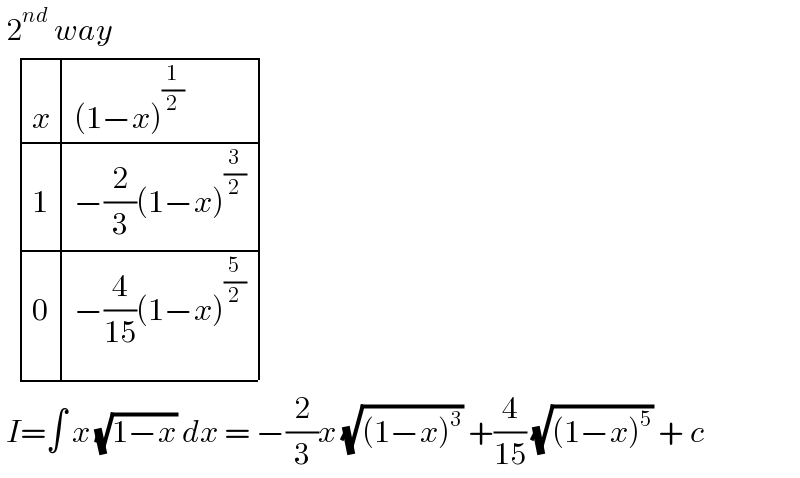 | ||
Answered by greougoury555 last updated on 03/May/22 | ||
![∫ x(√(1−x)) dx let (√(1−x)) = u → { ((x=1−u^2 )),((dx=−2u du)) :} I=∫ (1−u^2 )(u)(−2u)du =−2∫(1−u^2 )u^2 du =−2∫(u^2 −u^4 )du =−2[ (1/3)u^3 −(1/5)u^5 ]+c =−(2/(15))u^3 (5−3u^2 )+c =−(2/(15)) (√((1−x)^3 )) (5−3(1−x))+c =−(2/(15)) (3x+2)(√((1−x)^3 )) + c](Q169560.png) | ||
| ||