
Question and Answers Forum
Question Number 174276 by cortano1 last updated on 28/Jul/22

Answered by blackmamba last updated on 28/Jul/22
![lim_(x→0) ((1−((cos (2021x)))^(1/(2022)) )/x^2 ) = lim_(x→0) ((1−((1−2sin^2 (((2021x)/2))))^(1/(2022)) )/x^2 ) = lim_(x→0) ((1−(1−((2sin^2 (((2021x)/2)))/(2022))))/x^2 ) = (1/(1011)) ×lim_(x→0) [((sin (((2021x)/2)))/x) ]^2 = (1/(1011))×(((2021)^2 )/4) = ((2021^2 )/(4044))](Q174279.png)
Answered by Mathspace last updated on 28/Jul/22
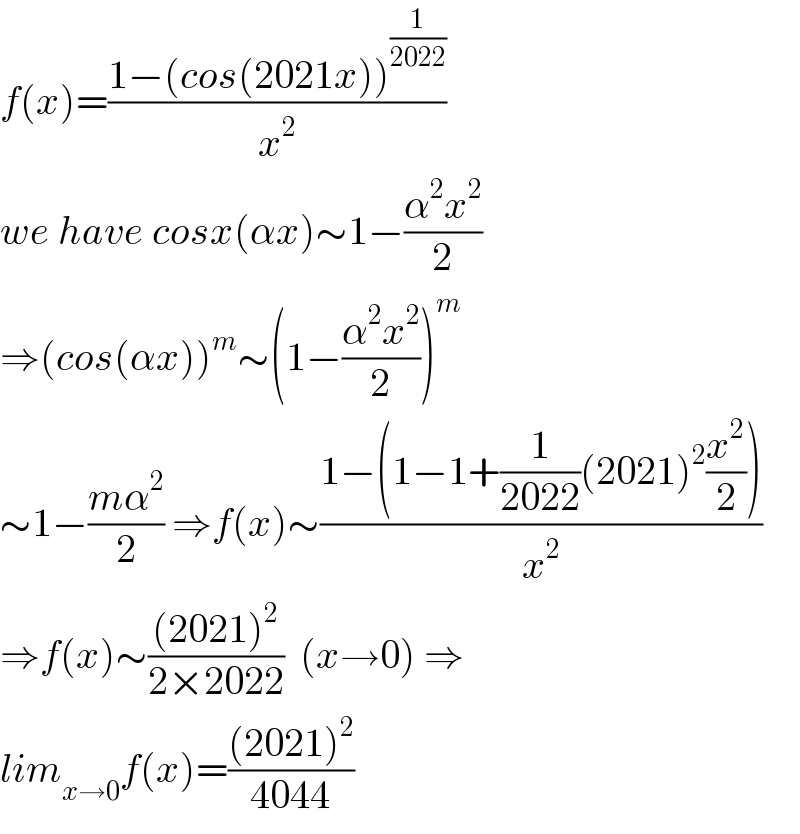
| ||
Question and Answers Forum | ||
Question Number 174276 by cortano1 last updated on 28/Jul/22 | ||
 | ||
Answered by blackmamba last updated on 28/Jul/22 | ||
![lim_(x→0) ((1−((cos (2021x)))^(1/(2022)) )/x^2 ) = lim_(x→0) ((1−((1−2sin^2 (((2021x)/2))))^(1/(2022)) )/x^2 ) = lim_(x→0) ((1−(1−((2sin^2 (((2021x)/2)))/(2022))))/x^2 ) = (1/(1011)) ×lim_(x→0) [((sin (((2021x)/2)))/x) ]^2 = (1/(1011))×(((2021)^2 )/4) = ((2021^2 )/(4044))](Q174279.png) | ||
| ||
Answered by Mathspace last updated on 28/Jul/22 | ||
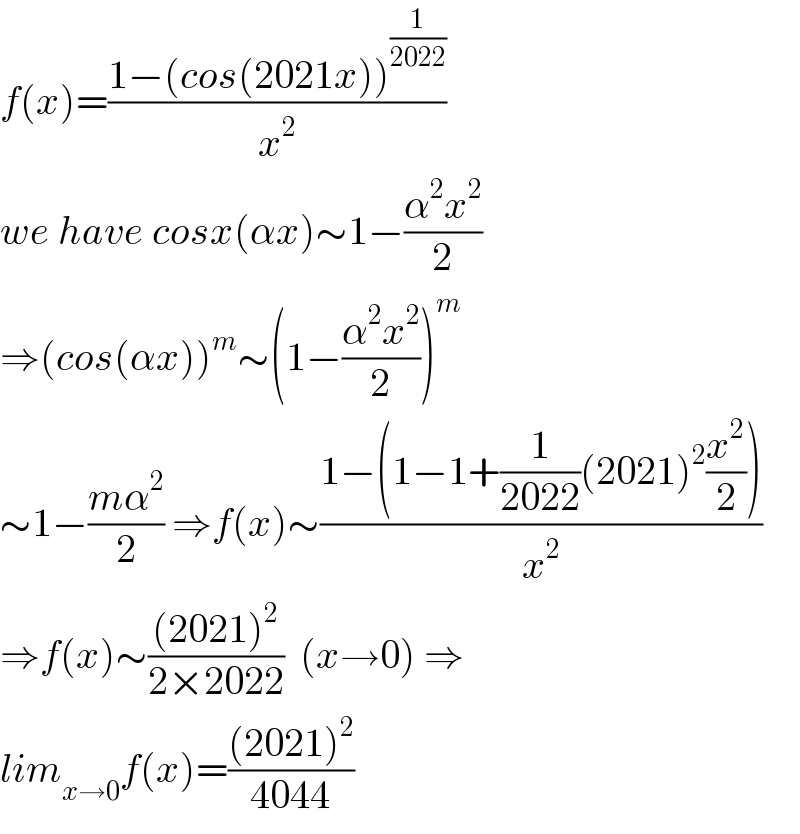 | ||
| ||