Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 177353 by HeferH last updated on 04/Oct/22

Commented by HeferH last updated on 04/Oct/22

$$:)$$

Answered by BaliramKumar last updated on 04/Oct/22

$$\frac{3}{13}???$$

Commented by mr W last updated on 04/Oct/22

$$yes!buthowdidyougetthat?$$

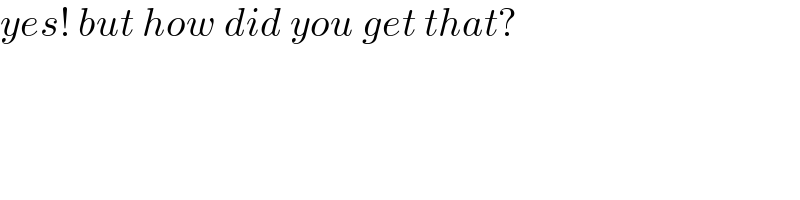
Commented by BaliramKumar last updated on 04/Oct/22

$$similartriangle\mathrm{\&}cosinerule$$$$seemysolution\downdownarrows$$

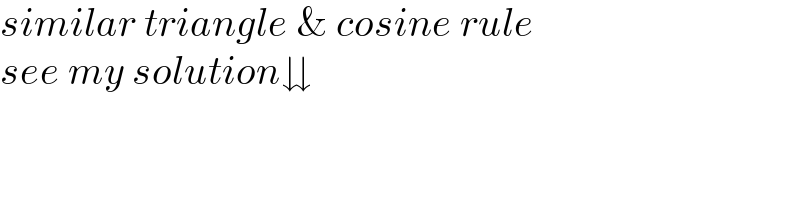
Answered by mr W last updated on 04/Oct/22

Commented by mr W last updated on 04/Oct/22

$$R=radius$$$$s=\sqrt{3}R$$$$\sin \alpha =\frac{x}{2R}$$$$\sin \beta =\frac{3x}{2R}$$$$\alpha +\beta =\frac{\pi }{3}$$$$\cos (\alpha +\beta )=\cos \frac{\pi }{3}=\frac{1}{2}$$$$\sqrt{(1-\frac{x^2}{4R^2})(1-\frac{9x^2}{4R^2})}-\frac{x}{2R}\times \frac{3x}{2R}=\frac{1}{2}$$$$\sqrt{(4R^2-x^2)(4R^2-9x^2)}=2R^2+3x^2$$$$16R^4-40R^2{x}^2+9x^4=4R^4+12R^2{x}^2+9x^4$$$$3R^2=13x^2$$$$\Rightarrow x=\sqrt{\frac{3}{13}}R$$$$\sin \beta =\frac{3x}{2R}=3\sqrt{\frac{3}{52}}\Rightarrow \cos \beta =\frac{5}{\sqrt{52}}$$$$\frac{b}{s}=\frac{\sin \frac{\pi }{3}}{\sin (\frac{\pi }{3}+\beta )}$$$$\frac{a+b}{s}=\frac{\sin (\frac{\pi }{3}+\beta )}{\sin \frac{\pi }{3}}$$$$\frac{a+b}{b}={\left[\frac{\sin (\frac{\pi }{3}+\beta )}{\sin \frac{\pi }{3}}\right]}^2={[\cos \beta +\frac{\sin \beta }{\tan \frac{\pi }{3}}]}^2$$$$\frac{a}{b}={[\cos \beta +\frac{\sin \beta }{\tan \frac{\pi }{3}}]}^2-1$$$$={[\frac{5}{\sqrt{52}}+\frac{3}{\sqrt{3}}\sqrt{\frac{3}{52}}]}^2-1$$$$={\left(\frac{8}{\sqrt{52}}\right)}^2-1=\frac{3}{13}✓$$

Commented by Tawa11 last updated on 04/Oct/22

$$\mathrm{Great}\mathrm{sir}$$

Answered by BaliramKumar last updated on 04/Oct/22

Commented by BaliramKumar last updated on 04/Oct/22

Commented by mr W last updated on 04/Oct/22

$$niceapproach!$$

Commented by BaliramKumar last updated on 04/Oct/22

$$thankssir$$

Commented by HeferH last updated on 04/Oct/22

$$Looksnice,IdiditbypureSimilar$$$$triangles$$

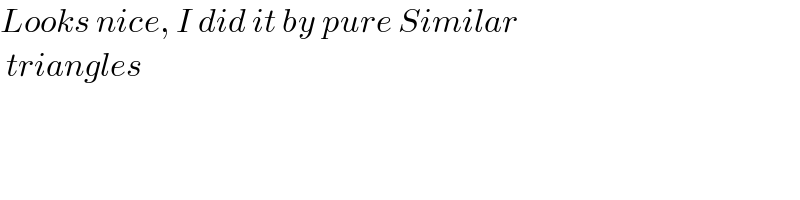
Answered by HeferH last updated on 04/Oct/22

Commented by HeferH last updated on 04/Oct/22

$$\bullet ab=c(d-c)$$$$\bullet \frac{3x}{d}=\frac{c}{b}\Rightarrow 3xb=dc(\mathbf{÷})$$$$\bullet \frac{x}{d}=\frac{a}{c}\Rightarrow xc=ad$$$$ab=\frac{c^2}{3}$$$$\frac{c^2}{3}=c(d-c)$$$$d=\frac{4c}{3}$$$$x=\frac{ad}{c}\Rightarrow x=\frac{4a}{3}$$$$\bullet \frac{a+b}{x}=\frac{4a}{a}$$$$(a+b)\cdot \frac{1}{a}=\frac{16a}{3}\cdot \frac{1}{a}$$$$1+\frac{b}{a}=\frac{16}{3}$$$$\frac{b}{a}=\frac{16-3}{3}=\frac{13}{3}\Rightarrow \frac{a}{b}=\frac{3}{13}$$$$$$

Commented by Tawa11 last updated on 04/Oct/22

$$\mathrm{Great}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com