
Question and Answers Forum
Question Number 177451 by mr W last updated on 05/Oct/22
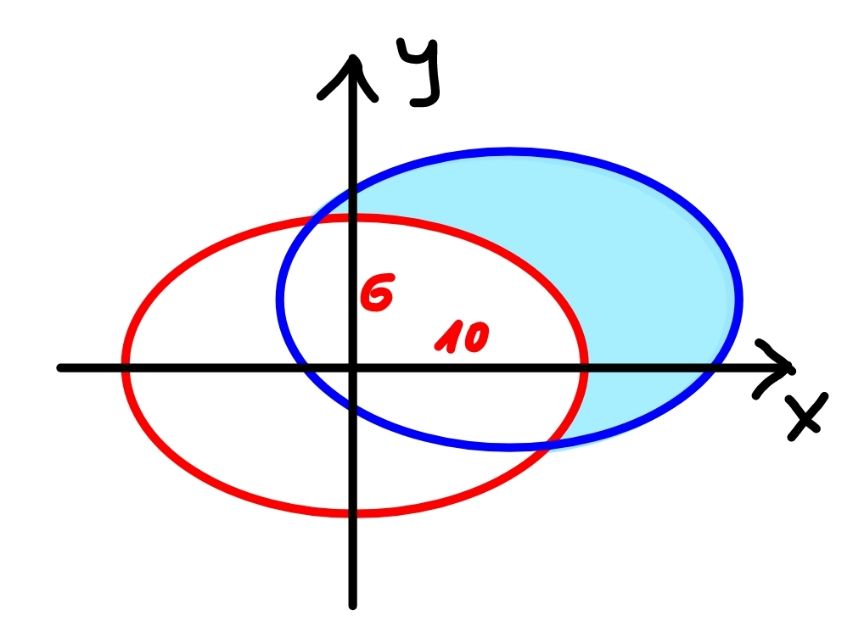
Commented by mr W last updated on 05/Oct/22

Answered by mr W last updated on 05/Oct/22
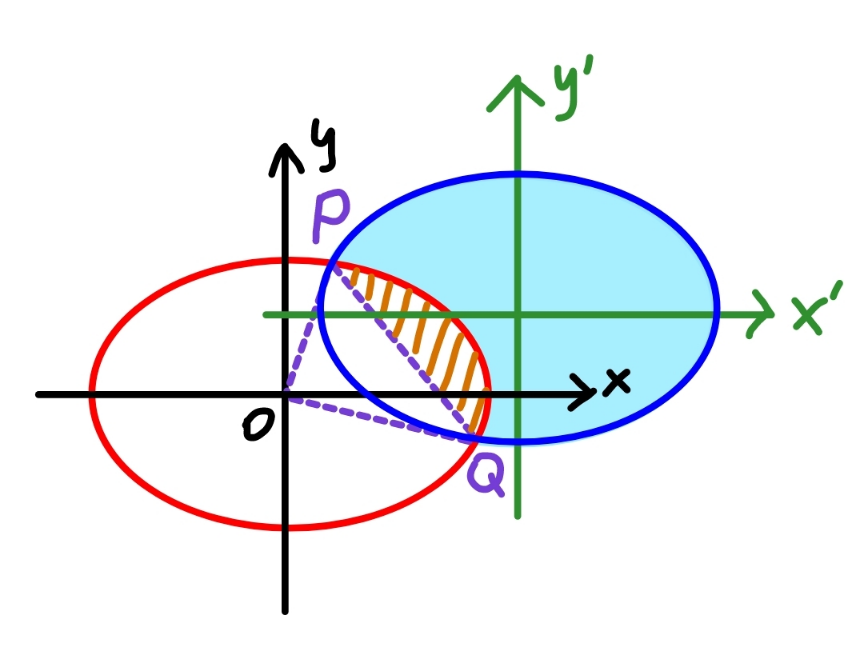
Commented by mr W last updated on 05/Oct/22
![red elipse: (x^2 /(10^2 ))+(y^2 /6^2 )=1 ⇒y=6(√(1−(x^2 /(100)))) blue elipse: (((x−5)^2 )/(10^2 ))+(((y−3)^2 )/6^2 )=1 line PQ: ((10x−25)/(10^2 ))+((6y−9)/6^2 )=0 ⇒y=3(1−(x/5)) point P and Q: (x^2 /(10^2 ))+(3^2 /6^2 )(1−(x/5))^2 =1 2x^2 −10x−75=0 x=((5±5(√7))/2) ⇒x_Q =((5(1+(√7)))/2), y_Q =((3(1−(√7)))/2) ⇒x_P =((5(1−(√7)))/2), y_P =((3(1+(√7)))/2) A_(segment) =∫_x_P ^x_Q [6(√(1−(x^2 /(100))))−3+((3x)/5)]dx+2∫_x_Q ^(10) 6(√(1−(x^2 /(100)))) dx =3∫_x_P ^x_Q [2(√(1−(x^2 /(100))))−1+(x/5)]dx+12∫_x_Q ^(10) (√(1−(x^2 /(100)))) dx =3[x(√(1−(x^2 /(100))))+10 sin^(−1) (x/(10))−x+(x^2 /(10))]_x_P ^x_Q +6[x(√(1−(x^2 /(100))))+10 sin^(−1) (x/(10))]_x_Q ^(10) =3{((5(1+(√7)))/2)(√(1−(((1+(√7))^2 )/(16))))−((5(1−(√7)))/2)(√(1−(((1−(√7))^2 )/(16))))+10( sin^(−1) ((1+(√7))/4)−sin^(−1) ((1−(√7))/4))−((5(1+(√7)−1+(√7)))/2)+((5[(1+(√7))^2 −(1−(√7))^2 ])/8)}+6{10(√(1−((100)/(100))))−((5(1+(√7)))/2)(√(1−(((1+(√7))^2 )/(16))))+10(sin^(−1) ((10)/(10))−sin^(−1) ((1+(√7))/4))} =((45)/2)+30( sin^(−1) ((1+(√7))/4)−sin^(−1) ((1−(√7))/4))−((15(√7))/2)−((45)/2)+30π−60 sin^(−1) ((1+(√7))/4) =30π−30( sin^(−1) ((1+(√7))/4)+ sin^(−1) ((1−(√7))/4))−((15(√7))/2) A_(elipse) =πab=10×6π=60π A_(shaded) =A_(elipse) −2A_(segment) =60π−60π+60(sin^(−1) ((1+(√7))/4)+sin^(−1) ((1−(√7))/4))+15(√7) =60(sin^(−1) ((1+(√7))/4)+ sin^(−1) ((1−(√7))/4))+15(√7) =60 cos^(−1) (3/4)+15(√7) ✓ ≈83.05](Q177472.png)
Commented by Ar Brandon last updated on 05/Oct/22
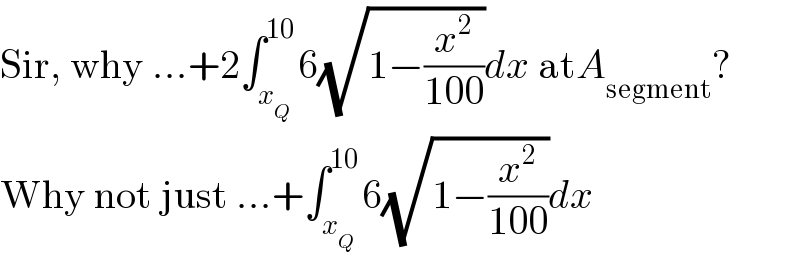
Commented by mr W last updated on 05/Oct/22

Commented by mr W last updated on 05/Oct/22
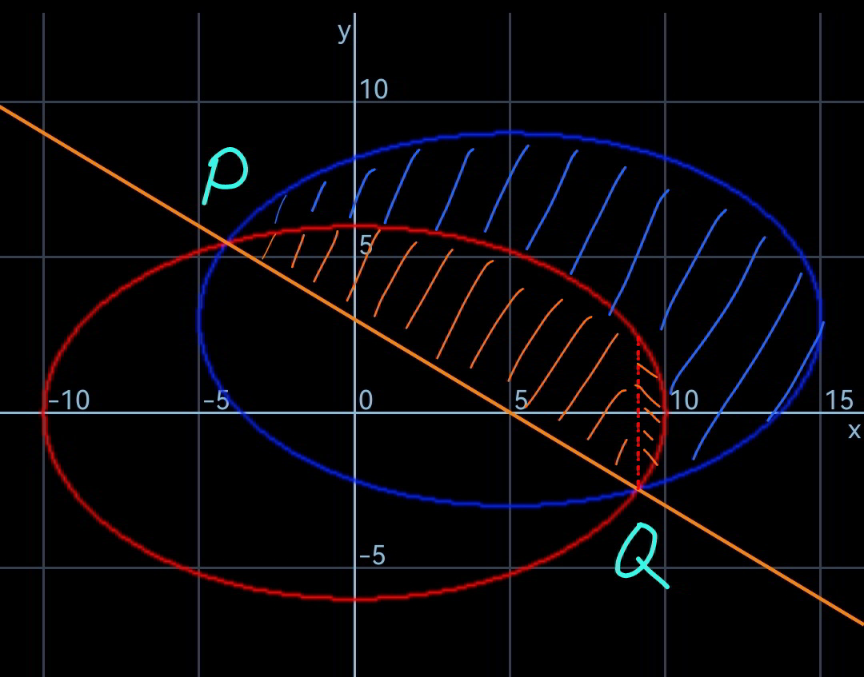
Commented by Ar Brandon last updated on 05/Oct/22

Commented by mr W last updated on 06/Oct/22

Commented by mr W last updated on 05/Oct/22
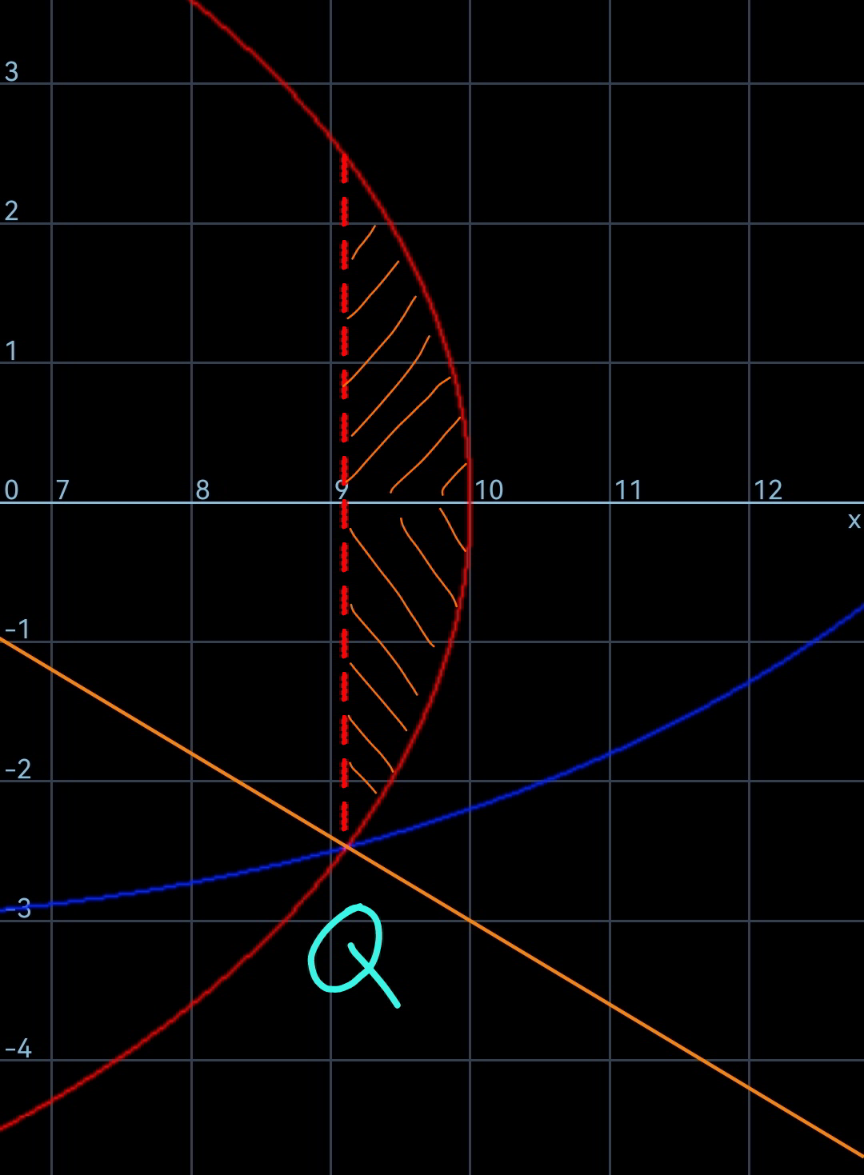
Commented by mr W last updated on 05/Oct/22

Commented by Ar Brandon last updated on 05/Oct/22
OK got it now. Thanks!
Commented by a.lgnaoui last updated on 05/Oct/22
![y_1 ^2 =(6^2 /(10^2 ))(100−x^2 ) (1) (y_2 +3)^2 =(6^2 /(10^2 ))[(100−(x+5)^2 ] (2) y_1 =y_2 (points communs (1)et(2) (1) y_1 =(6/(10))(√(100−x^2 )) (y+3)^2 =[3+(3/(10))(√(100−x^2 )) ]^2 =(9/(25))[(100−(x+5)^2 ] (9+((9/(25)))(100−x^2 )+((18)/5)(√(100−x^2 )) )=(9/(25))(75−x^2 −10x) (45−((9x^2 )/(25))+((18)/5)(√(100−x^2 )) )=(27−((9x^2 )/(25))−((18)/5)) 1+(1/5)(√(100−x^2 )) +(1/5)=0 x=9,92 ⇒intersection =(4,92 ; 9,92) y=(3/5)(√(100−24,20)) =5,22 P(4,92 ; 5,22) Q(9,92;−2,25) Aure=∫(6/5)+(1/5)(√(100−x^2 )) dx =(6/5)x+2∫(√(1−((x^2 /(10))))) dx sin t=(x/(10)) dx =10cos t dt=10(√(1−t^2 )) dt =10∫(1−t^2 ) dt=10t−10(t^3 /3) Aire=∫_0 ^5 =[((6x)/5) ]_0 ^5 +10[sin^(−1) ((x/(10)))]_0 ^5 −((10)/3)[(sin^(−1) ((x/(10))))^3 ]_0 ^5 =6+10sin^(−1) ((1/2))−((10)/3)[sin^(−1) ((1/2))]^3 6+2[10(π/6)−((10)/3)×(π^3 /(216))]=6+21,44−0,86 Aire=26,58 bj](Q177487.png)
Commented by mr W last updated on 05/Oct/22
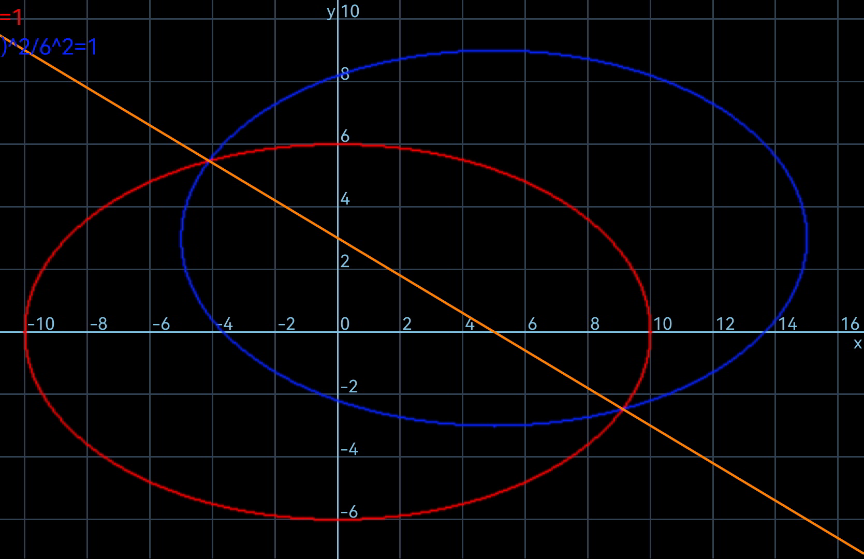
Commented by a.lgnaoui last updated on 05/Oct/22
Commented by Tawa11 last updated on 06/Oct/22

