Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 177675 by cortano1 last updated on 08/Oct/22

Commented by HeferH last updated on 08/Oct/22

${i s n}^{'} t 10 ?$ $4 x^{2} + x^{2} = 100$ $x^{2} = 20$ $A = \frac{20}{2} = 10 u^{2}$
Commented by som(math1967) last updated on 08/Oct/22

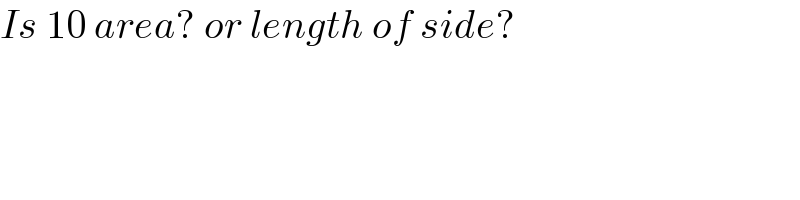
$I s 10 a r e a ? o r l e n g t h o f s i d e ?$
Commented by HeferH last updated on 08/Oct/22

$t h e g r e e n t r i a n g l e h a s t h e s a m e h e i g h t a n d$ $b a s e, s o w e n e e d \frac{x^{2}}{2} (‘ ‘ x^{″} w o u l d b e t h e$ $o r a n g e s e g m e n t)$
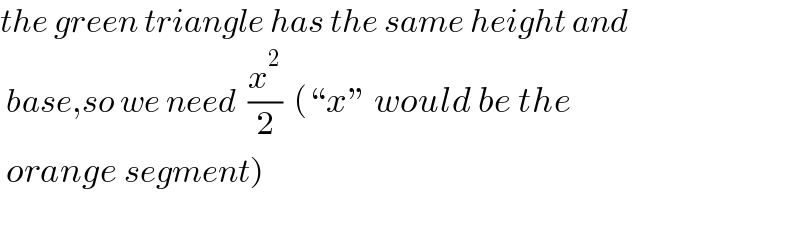
Commented by cortano1 last updated on 08/Oct/22

$the request is green area$
	Answered by som(math1967) last updated on 08/Oct/22

	$l e t B D = D C = x$ $B D = D E ∴ ∠ E B D = 45 \Rightarrow ∠ B A C = 45$ $∴ B C = A C = 2 x$ $4 x^{2} + x^{2} = 10^{2}$ $\Rightarrow x = 2 \sqrt{5}$ $a r . o f △ B D E = a r . △ A E D$ $[∵ D i s m i d p t o f B C, D E ∥ A C$ $∴ E i s m i d p t o f A B]$ $a r o f △ B D E = \frac{1}{2} \times 2 \sqrt{5} \times 2 \sqrt{5}$ $= 10 s q u n i t$ $A_{g r e e n} = 10 s q u n i t$ $[I f A D = 10]$
	Commented by som(math1967) last updated on 08/Oct/22

	Commented by HeferH last updated on 08/Oct/22

	$s o r r y i f I m i s u n d e r s t o o d y o u r q u e s t i o n s i r,$ $t h e y h a v e t h e s a m e c o l o r s o {i t}^{'} s p r o b a b l y$ $t h a t w a y .$
	Commented by Tawa11 last updated on 08/Oct/22

	$Great sir$
	Answered by Ar Brandon last updated on 08/Oct/22

	$x^{2} + 4 x^{2} = 10^{2} \Rightarrow x = 2 \sqrt{5}$ $A = \frac{2 x \times 2 x}{2} - \frac{x \times 2 x}{2} - \frac{x \times x}{2}$ $= 2 x^{2} - x^{2} - \frac{x^{2}}{2} = \frac{x^{2}}{2} = \frac{{(2 \sqrt{5})}^{2}}{2}$ $= 10 sq units$
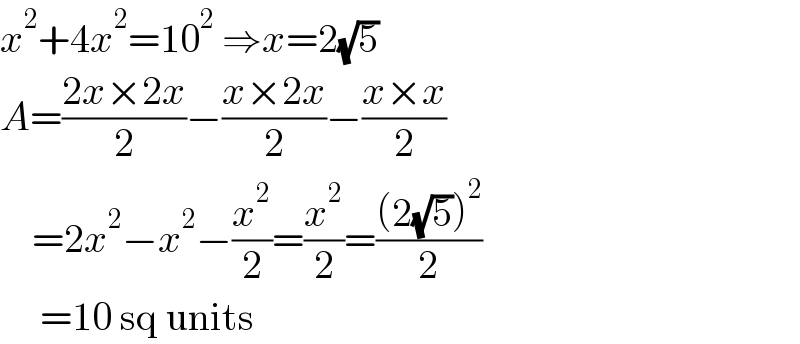
	Answered by a.lgnaoui last updated on 08/Oct/22

	$BD = DE \Rightarrow (∡ ABC = \frac{π}{4} DEB = \frac{3 π}{4})$ $Posons BD = x EC = y BE = x \sqrt{2}$ ${CD}^{2} = {ED}^{2} + {EC}^{2} - 2 ED \times ECcos 3 \frac{π}{4}$ $100 = x^{2} + y^{2} + \sqrt{2} x y (1)$ $\frac{\sin ∡ CDE}{y} = \frac{\sin 3 \frac{π}{4}}{10} (2)$ $∡ CDE = ∡ DCA \Rightarrow \sin (CDE) = \sin ∡ DCA = \frac{x}{10} (DE ∣∣ AB)$ $(1) \Rightarrow \frac{x}{10 y} = \frac{\sqrt{2}}{20} x = \frac{y \sqrt{2}}{2}$ $(1) \Leftrightarrow 100 = \frac{y^{2}}{2} + y^{2} + y^{2} = \frac{5 y^{2}}{2}$ $y = 2 \sqrt{10} x = 2 \sqrt{5} \sin ∡ C DE = \frac{\sqrt{5}}{5}$ $d o n c a i r e d e l a p a r r i e v e r t e$ $A i r e = 10 \times \frac{EH}{2} = 10 \frac{x \sin ∡ EDC}{2} = 5 \times 2 \sqrt{5} \times \frac{\sqrt{5}}{5}$ $A i r e = 10$
	Commented by a.lgnaoui last updated on 08/Oct/22

	Commented by a.lgnaoui last updated on 08/Oct/22

	$H \in CD \sin (∡ EDH) = \sin (∡ EDC) = \frac{EH}{ED}$
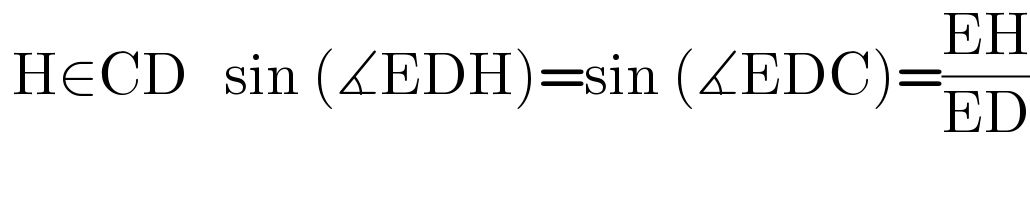
	Commented by Tawa11 last updated on 09/Oct/22

	$Great sirs .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum