Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 178923 by mnjuly1970 last updated on 22/Oct/22

Commented by mr W last updated on 22/Oct/22

$$\frac{6}{\sqrt[6]{108}}?$$

Commented by Frix last updated on 22/Oct/22

$$\frac{6}{\sqrt[6]{108}}=3^{\frac{1}{2}}{2}^{\frac{2}{3}}$$

Commented by mr W last updated on 23/Oct/22

$$thanksforcomfirming!$$

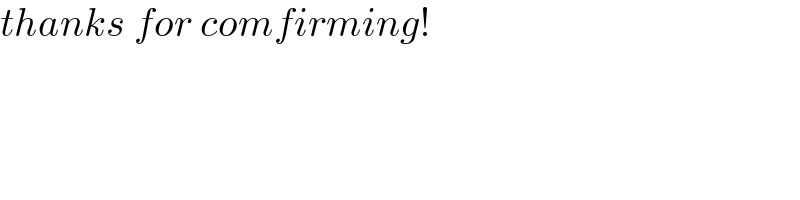
Answered by Frix last updated on 22/Oct/22

$$\mathrm{let}b=xa\wedge c=ya\wedge x,y>0$$$$f(a,b,c)=\frac{1}{x}+\frac{\sqrt{x}}{\sqrt{y}}+\sqrt[3]{y}$$$$\frac{d[\frac{1}{x}+\frac{\sqrt{x}}{\sqrt{y}}+\sqrt[3]{y}]}{dx}=0$$$$-\frac{1}{x^2}+\frac{1}{2\sqrt{xy}}=0\Rightarrow x=\sqrt[3]{4y}$$$$f(a,b,c)=\frac{3}{\sqrt[3]{4y}}+\sqrt[3]{y}$$$$\frac{d[\frac{3}{\sqrt[3]{4y}}+\sqrt[3]{y}]}{dy}=0$$$$-\frac{1}{\sqrt[3]{4y^4}}+\frac{1}{3\sqrt[3]{y^2}}=0\Rightarrow y=\frac{3\sqrt{3}}{2}\Rightarrow x=3^{\frac{1}{2}}{2}^{\frac{1}{3}}$$$$\Rightarrow \max \left(f\right)=3^{\frac{1}{2}}{2}^{\frac{2}{3}}$$

Answered by mr W last updated on 22/Oct/22

$$let\frac{c}{a}=r^3,\frac{b}{c}=q^2,\frac{a}{b}=p$$$$\frac{a}{b}\times \frac{b}{c}\times \frac{c}{a}={pq}^2{r}^3=1$$$$f(p,q,r)=p+q+r$$$$F(p,q,r)=p+q+r+\lambda ({pq}^2{r}^3-1)$$$$\frac{\partial F}{\partial p}=1+\lambda q^2{r}^3=0$$$$\Rightarrow p=-\lambda$$$$\frac{\partial F}{\partial q}=1+2\lambda {pqr}^3=0$$$$\Rightarrow q=-2\lambda$$$$\frac{\partial F}{\partial r}=1+3\lambda {pq}^2{r}^2=0$$$$\Rightarrow r=-3\lambda$$$$(-\lambda ){(-2\lambda )}^2{(-3\lambda )}^3=1$$$$108{\lambda }^6=1$$$${\lambda }^6=\frac{1}{108}\Rightarrow \lambda =-\frac{1}{\sqrt[6]{108}}$$$$f_{min}=-\lambda -2\lambda -3\lambda =-6\lambda =\frac{6}{\sqrt[6]{108}}✓$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com