Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 181812 by HeferH last updated on 01/Dec/22

Answered by mr W last updated on 01/Dec/22

$$\sin 30°=\frac{\sin (2\alpha +30°)}{2\cos \alpha }$$$$\sin (2\alpha +30°)=\cos \alpha =\sin (90°-\alpha )$$$$2\alpha +30°=90°-\alpha \Rightarrow \alpha =20°$$$$or$$$$2\alpha +30°=90°+\alpha \Rightarrow \alpha =60°$$

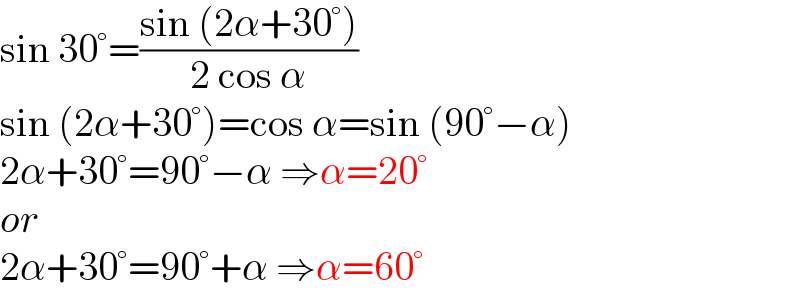
Commented by mr W last updated on 01/Dec/22

Commented by mr W last updated on 01/Dec/22

Answered by som(math1967) last updated on 01/Dec/22

$$letAD=DC=x,AC=BD=y$$$$from△ADC\frac{x}{sin\alpha }=\frac{y}{sin(180-2\alpha )}$$$$\Rightarrow x=\frac{ysin\alpha }{sin2\alpha }=\frac{y}{2cos\alpha }[sin2\alpha =2sin\alpha cos\alpha ]$$$$from△ABD$$$$\frac{x}{sin30}=\frac{y}{sin(180-30-2\alpha )}$$$$\Rightarrow \frac{y}{2sin30cos\alpha }=\frac{y}{sin(150-2\alpha )}$$$$\Rightarrow \frac{1}{cos\alpha }=\frac{1}{sin(150-2\alpha )}$$$$\Rightarrow sin(90-\alpha )=sin(150-2\alpha )$$$$\Rightarrow 90-\alpha =150-2\alpha$$$$\Rightarrow 2\alpha -\alpha =150-90$$$$\therefore \alpha =60$$$$or$$$$sin(90+\alpha )=sin(150-2\alpha )$$$$90+\alpha =150-2\alpha$$$$\Rightarrow 3\alpha =60\therefore \alpha =20$$

Commented by som(math1967) last updated on 01/Dec/22

Answered by Acem last updated on 01/Dec/22

Commented by Acem last updated on 01/Dec/22

$$5\alpha =187.5ineedrecheckmysolution$$

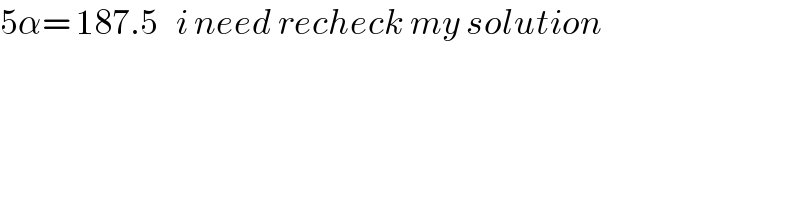
Answered by HeferH last updated on 01/Dec/22

Commented by HeferH last updated on 01/Dec/22

$$2\alpha -60°=\alpha$$$$\alpha =60°$$$$thankyouallforanswering,Iwantedtosee$$$$othermethods:)$$

Answered by a.lgnaoui last updated on 01/Dec/22

$$\frac{\sin 30}{\mathrm{BC}}=\frac{\sin \lambda }{\mathrm{AC}}\mathrm{BC}=\frac{\mathrm{AC}\times \sin 30}{\sin \lambda }$$$$\text{Missing left or extra right}$$$$\mathrm{AC}=\mathrm{BD}\Rightarrow =$$$$\frac{\sin \alpha }{\mathrm{BC}}=\frac{\sin 2\alpha }{\mathrm{AC}}\Rightarrow \frac{\sin \alpha }{\frac{\mathrm{AC}\times \sin 30}{\sin \lambda }}=\frac{\sin 2\alpha }{\mathrm{AC}}$$$$\frac{\sin \alpha \times \sin \lambda }{\sin 30}=\sin 2\alpha$$$$\sin \lambda =\frac{\sin 30\times \sin 2\alpha }{\sin \alpha }=\cos \alpha =$$$$\lambda =\frac{\pi }{2}-\alpha \left(1\right)$$$$\theta =\pi -2\alpha$$$$△\mathrm{ABD}$$$$2\alpha +\lambda +30=180$$$$\lambda =150-2\alpha \left(2\right)$$$$\left(1\right)\mathrm{et}\left(2\right)\Rightarrow 90-\alpha =150-2\alpha$$$$\alpha =150-90$$$$Angle\alpha =60°$$$$$$

Commented by a.lgnaoui last updated on 01/Dec/22

Terms of Service

Privacy Policy

Contact: info@tinkutara.com