Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 182500 by mr W last updated on 10/Dec/22

Commented by mr W last updated on 10/Dec/22

$$thistimeourgoatisflexiblytiedon$$$$afencewitharopeoflength3m.the$$$$fencehastheshapeofanellipsewith$$$$semi-axexof10mand6mrespectively.$$$$findthemaximumareawherethe$$$$goatcangraze.$$

Answered by mr W last updated on 10/Dec/22

Commented by mr W last updated on 10/Dec/22

$$a=10,b=6,c=3$$$$let\mu =\frac{b}{a},\lambda =\frac{c}{a}$$$$sayP(a\cos \varphi ,b\sin \varphi )$$$$-\frac{1}{\tan \theta }=\frac{b\cos \varphi }{-a\sin \theta }$$$$\Rightarrow \tan \theta =\frac{\tan \varphi }{\mu }$$$$x_Q=a\cos \varphi +c\cos \theta$$$$y_Q=b\sin \varphi +c\sin \theta$$$$\frac{x_Q}{a}=\xi =\cos \varphi +\frac{\lambda \mu }{\sqrt{{\mu }^2+{\tan }^2\varphi }}$$$$\frac{y_Q}{a}=\eta =\mu \sin \varphi +\frac{\lambda \tan \varphi }{\sqrt{{\mu }^2+{\tan }^2\varphi }}$$$$A_I=\int y_Q{dx}_Q$$$$\frac{A_I}{a^2}=\int \eta d\xi ={\int }_0^{\frac{\pi }{2}}(\mu \sin \varphi +\frac{\lambda \tan \varphi }{\sqrt{{\mu }^2+{\tan }^2\varphi }})(\sin \varphi +\frac{\lambda \mu \tan \varphi }{{\cos }^2\varphi {({\mu }^2+{\tan }^2\varphi )}^{3/2}})d\varphi =\delta$$$$\delta ={\int }_0^{\frac{\pi }{2}}(\mu \sin \varphi +\frac{\lambda \tan \varphi }{\sqrt{{\mu }^2+{\tan }^2\varphi }})(\sin \varphi +\frac{\lambda \mu \tan \varphi }{{\cos }^2\varphi {({\mu }^2+{\tan }^2\varphi )}^{3/2}})d\varphi$$$$A_{grazing}=4A_I-\pi ab=4\delta a^2-\pi ab$$$$A_{grazing}=(\frac{4\delta }{\mu }-\pi )ab$$$$example:$$$$\mu =\frac{6}{10}=0.6,\lambda =\frac{3}{10}=0.3$$$$\delta \approx 0.924829716$$$$A_{grazing}=(\frac{4\delta }{0.6}-\pi )\times 60\approx 181.436m^2$$$$$$$$anapproximationasellipseis$$$$A_{grazing}\approx \pi [(a+c)(b+c)-ab]=\pi (a+b+c)c$$$$=(10+6+3)\pi =179.07m^2$$

Commented by mr W last updated on 10/Dec/22

Commented by mr W last updated on 10/Dec/22

$$weseethegrazingareaisveryclose$$$$toaperfectellipse\frac{x^2}{{(a+c)}^2}+\frac{y^2}{{(b+c)}^2}=1.$$

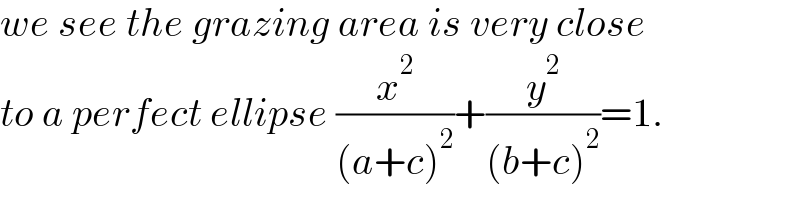
Commented by Acem last updated on 10/Dec/22

$$Sonice$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com