Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 182973 by HeferH last updated on 17/Dec/22

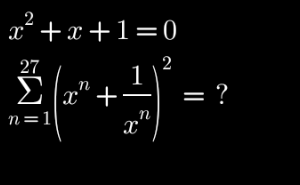
Answered by Rasheed.Sindhi last updated on 18/Dec/22

$$x^2+x+1=0;\underset{n=1}{\stackrel{27}{\mathrm{\Sigma }}}{(x^n+\frac{1}{x^n})}^2=?$$$${(x^n+\frac{1}{x^n})}^2=x^{2n}+\frac{1}{x^{2n}}+2$$$$S_{27}=\underset{n=1}{\sum ^{27}}{(x^n+\frac{1}{x^n})}^2=\underset{n=1}{\stackrel{27}{\mathrm{\Sigma }}}{x}^{2n}+\underset{n=1}{\stackrel{27}{\mathrm{\Sigma }}}\frac{1}{x^{2n}}+\underset{n=1}{\stackrel{27}{\mathrm{\Sigma }}}2$$$$=27\left(2\right)+(x^2+x^4+x^6+...x^{54})+(x^{-2}+x^{-4}+x^{-6}+...x^{-54})$$$$=54+\frac{x^2(1-{\left(x^2\right)}^{27})}{1-x^2}+\frac{x^{-2}(1-{\left(x^{-2}\right)}^{27})}{1-x^{-2}}$$$$=54+\frac{x^2-x^{56}}{1-x^2}+\frac{x^{-2}-x^{-56}}{1-x^{-2}}★$$$$$$$$x^2+x+1=0\Rightarrow x^2=-x-1$$$$\Rightarrow x^3=-x^2-x=-(-x-1)-x=1$$$$\Rightarrow x^3=1$$$$\bullet x^{56}={\left(x^3\right)}^{18}\cdot x^2=1^{18}(-x-1)=-x-1$$$$\bullet x^{-56}={\left(x^3\right)}^{-19}\cdot x={\left(1\right)}^{-19}\cdot x=x$$$$\bullet x^{-2}={\left(x^3\right)}^{-1}\cdot x={\left(1\right)}^{-1}\cdot x=x$$$$$$$$S_{27}=54+\frac{x^2-x^{56}}{1-x^2}+\frac{x^{-2}-x^{-56}}{1-x^{-2}}$$$$=54+\frac{(-x-1)-(-x-1)}{1-(-x-1)}+\frac{\left(x\right)-\left(x\right)}{1-\left(x\right)}$$$$=54$$

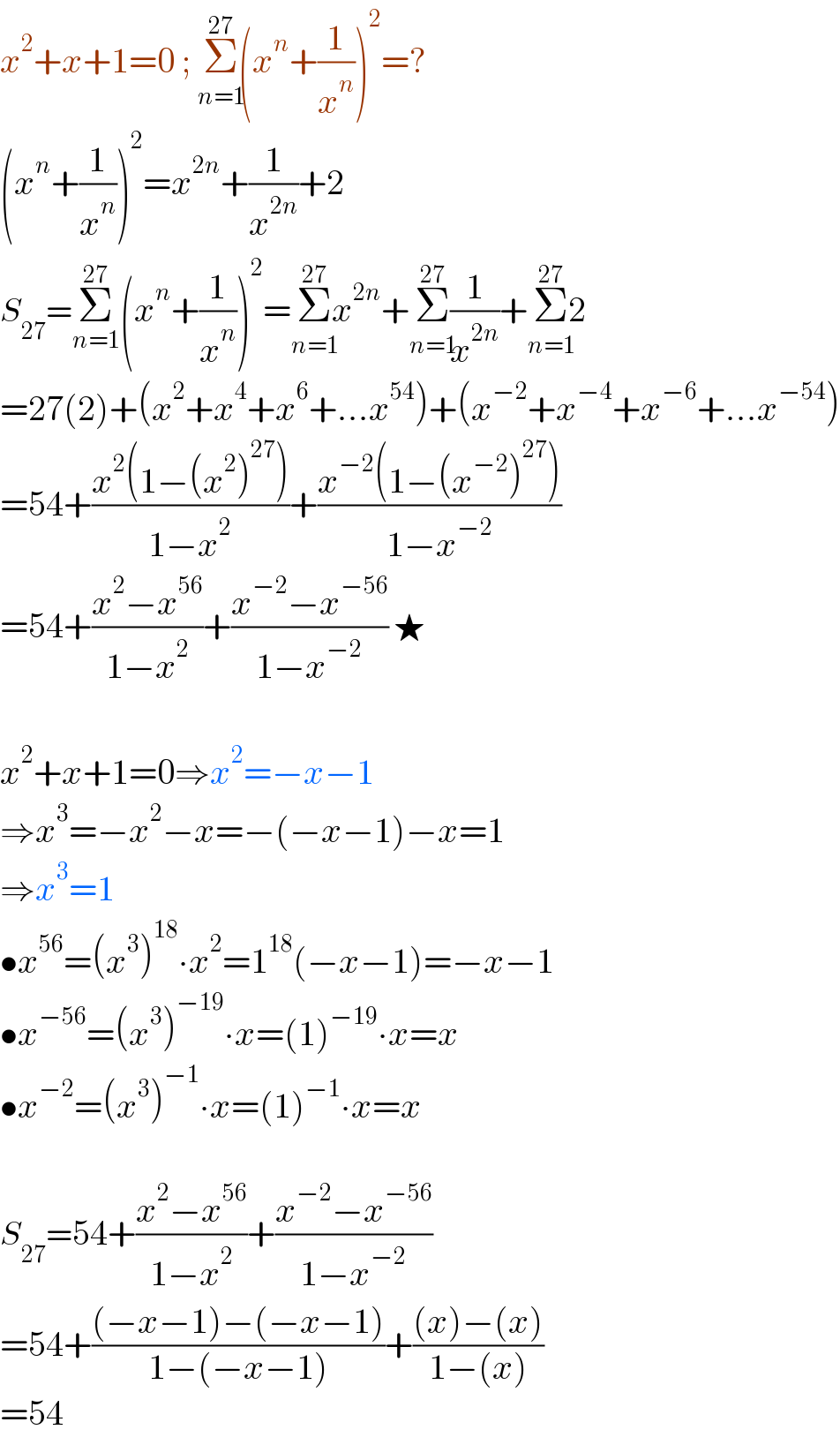
Commented by Rasheed.Sindhi last updated on 18/Dec/22

$$\mathrm{Or}\mathrm{in}\mathrm{somewhat}\mathrm{shorter}\mathrm{way}$$$$★S_{27}=54+\frac{x^2-x^{56}}{1-x^2}+\frac{x^{-2}-x^{-56}}{1-x^{-2}}$$$$$$$$x^2+x+1=0\Rightarrow x^2=-x-1$$$$\Rightarrow x^3=-x^2-x=-(-x-1)-x=1$$$$$$$$S_{27}=54+\frac{x^2-{\left(x^3\right)}^{18}\cdot x^2}{1-x^2}+\frac{x^{-2}-{\left(x^3\right)}^{-18}\cdot x^{-2}}{1-x^{-2}}$$$$S_{27}=54+\frac{x^2-{\left(1\right)}^{18}\cdot x^2}{1-x^2}+\frac{x^{-2}-{\left(1\right)}^{-18}\cdot x^{-2}}{1-x^{-2}}$$$$S_{27}=54+\frac{\cancel{x^2}-\cancel{x^2}}{1-x^2}+\frac{\cancel{x^{-2}}-\cancel{x^{-2}}}{1-x^{-2}}$$$$=54$$

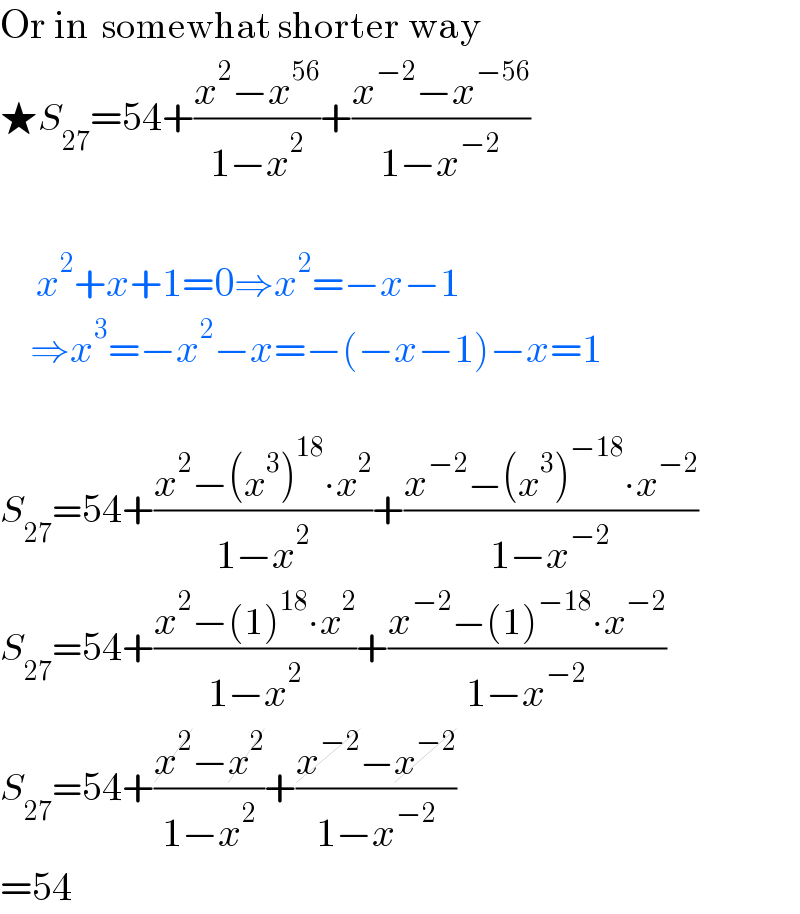
Answered by TANMAY PANACEA last updated on 18/Dec/22

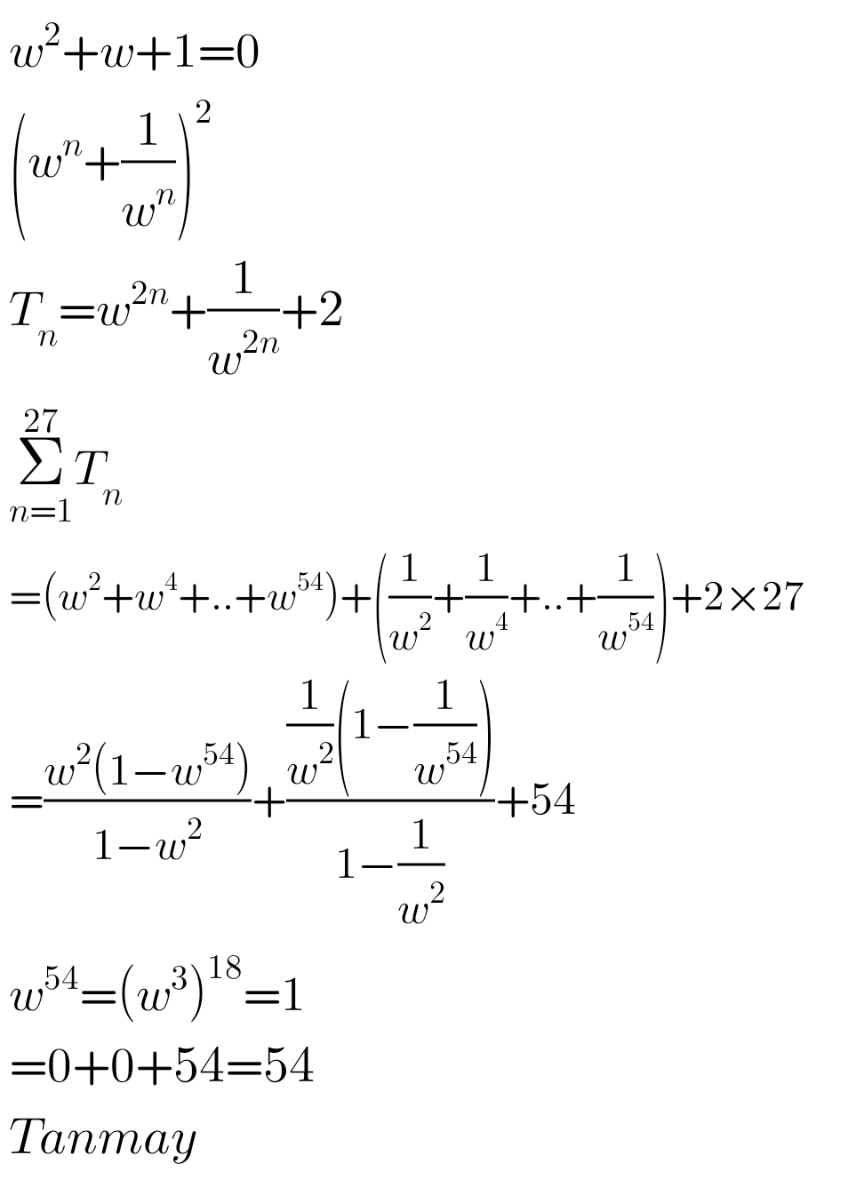
Commented by mr W last updated on 18/Dec/22

$$welcomebacksir!$$$$youseemtohavetakenalongbreak.$$

Commented by Rasheed.Sindhi last updated on 18/Dec/22

$$\mathcal{T}anmaysir,happytoseeyouagain!$$

Answered by TheSupreme last updated on 18/Dec/22

$$x+1+\frac{1}{x}=0\to \frac{1}{x}=-x-1$$$$\underset{n=1}{\sum ^{27}}{x}^{2n}+\frac{1}{x^{2n}}+2=$$$$=\frac{1-x^{2\ast 27-1}}{1-x}-1+\frac{1-\frac{1}{x^{2\ast 27-1}}}{1-\frac{1}{x}}-1+2\cdot 27=$$$$=\frac{1-x^{53}}{1-x}-\frac{1-x^{53}}{x^{52}(1-x)}+52$$$$=\frac{1-x^{53}}{1-x}[1-\frac{1}{x^{52}}]+52=$$$$=$$$$x^2+x+1=0\to x_{1,2}=\frac{-1\pm \sqrt{-3}}{2}=e^{\pm \frac{\pi }{3}i}$$$$\mathrm{\Sigma }{(e^{k\frac{\pi }{3}i}+e^{-k\frac{\pi }{3}i})}^2=\mathrm{\Sigma }4{cos}^2\left(k\frac{\pi }{3}\right)=$$$$=\underset{n=1}{\sum ^9}4{cos}^2\left(0\right)+4{cos}^2\left(\frac{\pi }{3}\right)+4{cos}^2\frac{2\pi }{3}=$$$$=4\underset{n=1}{\sum ^9}1+\frac{1}{4}+\frac{1}{4}=6\cdot 9=54$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com