Math Question and Answers


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 183711 by Michaelfaraday last updated on 29/Dec/22

Commented by Matica last updated on 29/Dec/22

$t o m a t h e m a t i z e$
	Answered by HeferH last updated on 29/Dec/22

	$\sqrt[3]{x^{2} \sqrt[3]{x^{2} \sqrt[3]{x^{2} . . .}}} = H$ $\sqrt[3]{x^{2} H} = H$ ${H x}^{2} = H^{3}$ $x = H$ $\sqrt{x^{2} + x \sqrt{x^{2} + x \sqrt{x^{2} + x \sqrt{. . .}}}} = P$ $\sqrt{x^{2} + x \cdot P} = P$ $x^{2} + P x = P^{2}$ $x^{2} + P x - P^{2} = 0$ $\frac{x}{P} + 1 - \frac{P}{x} = 0$ $l e t \frac{x}{P} = t$ $t + 1 - \frac{1}{t} = 0$ $t^{2} + t - 1 = 0$ $t = \frac{- 1 \pm \sqrt{1 - 4 (1) (- 1)}}{2 (1)} = \frac{- 1 \pm \sqrt{5}}{2}$ $\frac{x}{P} = \frac{- 1 + \sqrt{5}}{2}$ $\frac{2 x}{\sqrt{5} - 1} = P \Rightarrow$ $\frac{x}{\frac{2 x}{\sqrt{5} - 1}} = \frac{x}{5} \Rightarrow \frac{2 x}{\sqrt{5} - 1} = 5$ $x = \frac{5 \sqrt{5} - 5}{2}$
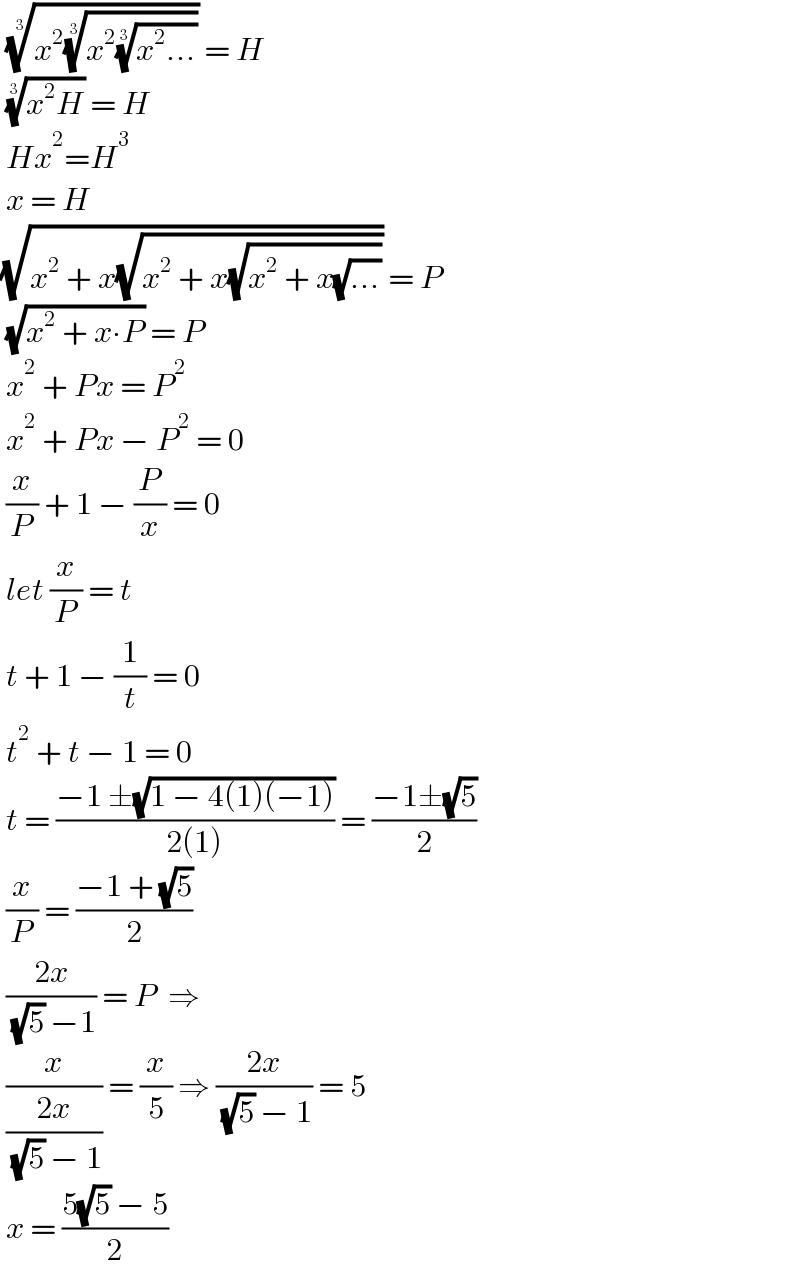
	Commented by JDamian last updated on 29/Dec/22

	$I n t h i s s t e p$ $x^{2} + P x = P^{2}$ $w h y {d o n}^{'} t y o u s o l v e q u i c k l y a s a q u a d r a t i c$ $e q u a t i o n ? Y o u h a v e c h a n g e d i n t o a n o t h e r$ $q u a d r a t i c e q u a t i o n i n t a n d s o l v e d t o g e t P,$ $w h i c h i s u n n e c e s s a r y .$
	Commented by Michaelfaraday last updated on 29/Dec/22

	$t h a n k s s i r$ $b u t s i r i t h i n k y o u s h o u l d h a v e s o l v e i t$ $i n f o r m o f q u a d r a t i c e q n f r o m$ $x^{2} + p x - p^{2} = 0 w h i l e y o u r s o l v i n g f r o m e q n$ $w h i c h i s n o t n e c e s s a r y .$
	Commented by HeferH last updated on 29/Dec/22

	$Y e a h y o u a r e r i g h t, i n m y d e f e n s e$ $i t w a s v e r y l a t e (00 : 48) w h e n i d i d i t$
	Commented by Michaelfaraday last updated on 29/Dec/22

	$o k a y s i r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum