Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 20230 by ajfour last updated on 24/Aug/17

Commented by ajfour last updated on 27/Aug/17

$F i n d t h e a r e a o f t h a t p a r t o f t h e$ $s u r f a c e o f t h e s p h e r e :$ $x^{2} + y^{2} + z^{2} = a^{2} w h i c h i s c u t o u t b y$ $t h e s u r f a c e o f t h e c y l i n d e r :$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b) .$
Commented by ajfour last updated on 26/Aug/17

$I {c o u l d n}^{'} t s o l v e t h i s, m e t h o d i s$ $c l e a r t o m e, b u t t h e i n t e g r a l i$ $c a n n o t s i m p l i f y . m r W 1 S i r,$ $p l e a s e h e l p a f t e r i a t t a c h a$ $d i a g r a m f o r i t s s o l u t i o n .$
Commented by ajfour last updated on 26/Aug/17

Commented by ajfour last updated on 26/Aug/17

$L e t A r e a o f s p h e r e o u t s i d e$ $c y l i n d e r b e A .$ $A = 2 \int_{- θ_{0}}^{θ_{0}} r (2 ϕ) a d θ$ $w h e r e a \cos θ_{0} = b$ $r^{2} = x^{2} + y^{2} s u c h t h a t$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 a n d a l s o r = a \cos θ$ $a n d \tan ϕ = \frac{x}{y} .$ $P l e a s e h e l p e v a l u a t i n g t h e i n t e g r a l . .$
Commented by ajfour last updated on 26/Aug/17

$x = y \tan ϕ$ $x^{2} + y^{2} = y^{2} (1 + \tan^{2} ϕ) = r^{2} . . . (i ($ $\frac{y^{2} \tan^{2} ϕ}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $y^{2} (\frac{\tan^{2} ϕ}{a^{2}} + \frac{1}{b^{2}}) = 1 . . . . (i i)$ $d i v i d i n g (i) b y (i i) :$ $\frac{1 + \tan^{2} ϕ}{\frac{\tan^{2} ϕ}{a^{2}} + \frac{1}{b^{2}}} = r^{2} \Rightarrow \tan^{2} ϕ = \frac{(\frac{r^{2}}{b^{2}} - 1)}{(1 - \frac{r^{2}}{a^{2}})}$ $1 + \tan^{2} ϕ = \frac{r^{2} (\frac{1}{b^{2}} - \frac{1}{a^{2}})}{(1 - \frac{r^{2}}{a^{2}})}$ $a s r = a \cos θ$ $\sec^{2} ϕ = \frac{\cos^{2} θ (a^{2} - b^{2})}{b^{2} \sin^{2} θ}$ $\Rightarrow \cos ϕ = \frac{b \tan θ}{\sqrt{a^{2} - b^{2}}}$ $\Rightarrow ϕ = \cos^{- 1} (\frac{b \tan θ}{\sqrt{a^{2} - b^{2}}})$ $A = 8 a \int_{0}^{θ_{0}} r ϕ d θ = 8 a (I)$ $I = \int_{0}^{θ_{0}} a \cos θ \cos^{- 1} (\frac{b \tan θ}{\sqrt{a^{2} - b^{2}}}) d θ$ $= a \sin θ \cos^{- 1} (\frac{b \tan θ}{\sqrt{a^{2} - b^{2}}}) ∣_{0}^{θ_{0}}$ $- \frac{- b}{\sqrt{a^{2} - b^{2}}} \int_{0}^{θ_{0}} \frac{(a \sin θ \sec^{2} θ) d θ}{\sqrt{1 - \frac{b^{2} \tan^{2} θ}{(a^{2} - b^{2})}}}$ $a n d a s a \cos θ_{0} = b$ $\tan θ_{0} = \frac{\sqrt{a^{2} - b^{2}}}{b}, s o$ $I = 0 + a b \int_{0}^{θ_{0}} \frac{\sec θ \tan θ d θ}{\sqrt{a^{2} - b^{2} - b^{2} \tan^{2} θ}}$ $= a \int_{0}^{θ_{0}} \frac{d (b \sec θ)}{\sqrt{a^{2} - b^{2} \sec^{2} θ}}$ $= a \sin^{- 1} (\frac{b \sec θ}{a}) ∣_{0}^{θ_{0}}$ $= a [\sin^{- 1} (\frac{b}{a \cos θ_{0}}) - \sin^{- 1} (\frac{b}{a})]$ $b u t a \cos θ_{0} = b, s o$ $I = a [\frac{π}{2} - \sin^{- 1} \frac{b}{a}]$ $a n d$ $A = 8 a^{2} [\frac{π}{2} - \sin^{- 1} \frac{b}{a}]$ $A = 4 π a^{2} - 8 a^{2} \sin^{- 1} (\frac{b}{a}) .$ $(s t i l l a n s w e r d o n t m a t c h)$ $H e l p!$
	Answered by ajfour last updated on 25/Aug/17

	$A r e a = 4 π a^{2} - 8 a^{2} \sin^{- 1} (\frac{\sqrt{a^{2} - b^{2}}}{a}) .$
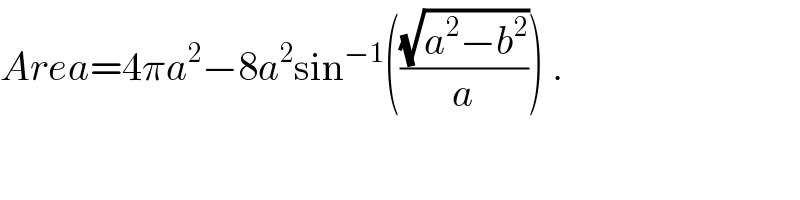
	Commented by ajfour last updated on 26/Aug/17

	$T h i s i s t b e a n s w e r i n b o o k .$ $i f b \to a t h e n A r e a s h o u l d t e n d$ $t o z e r o . T h i s i s f u l f i l l e d b y m y$ $a n s w e r .$ $i f b \to 0 A r e a s h o u l d t e n d t o 4 π r^{2},$ $a g a i n t h i s i s f u l f i l l e d b y m y$ $a n s w e r . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum