
Question and Answers Forum
Question Number 20488 by xing last updated on 27/Aug/17
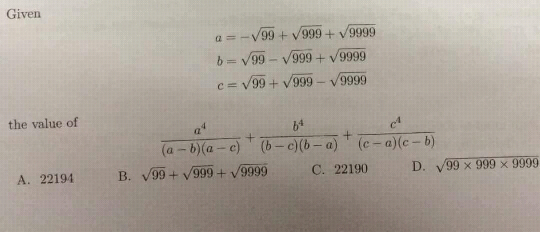
Commented by ajfour last updated on 27/Aug/17
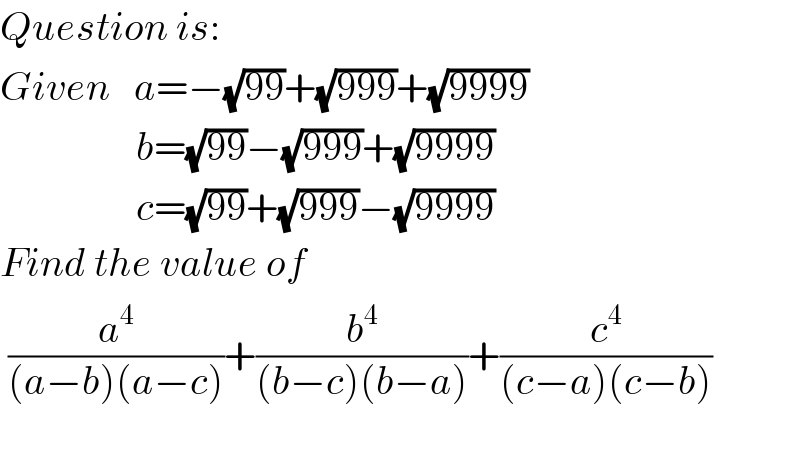
Answered by ajfour last updated on 27/Aug/17
![Let a=pc , b=qc ; then (a^4 /((a−b)(a−c)))+(b^4 /((b−c)(b−a)))+(c^4 /((c−a)(c−b))) =((p^4 c^4 )/(c^2 (p−q)(p−1)))+((q^4 c^4 )/(c^2 (q−1)(q−p))) +(c^4 /(c^2 (1−p)(1−q))) =(c^2 /((p−q)))[(p^4 /(p−1))−(q^4 /(q−1))+((p−q)/((1−p)(1−q)))] =(c^2 /((p−q)))[((p^4 q−p^4 −pq^4 +q^4 +p−q)/((1−p)(1−q)))] =(c^2 /((p−q)))[((pq(p^3 −q^3 )−(p^4 −q^4 )+(p−q))/((1−p)(1−q)))] =c^2 [((pq(p^2 +q^2 +pq)−(p^2 +q^2 )(p+q)+1)/((1−p)(1−q)))] =c^2 [(((p^2 +q^2 )(pq−p−q)+p^2 q^2 +1)/((1−p)(1−q)))] =c^2 [(((p^2 +q^2 )(p−1)(q−1)−p^2 −q^2 +p^2 q^2 +1)/((1−p)(1−q)))] =c^2 [(((p^2 +q^2 )(p−1)(q−1)+(p^2 −1)(q^2 −1))/((1−p)(1−q)))] =c^2 [p^2 +q^2 +(p+1)(q+1)] =c^2 [p^2 +q^2 +pq+p+q+1] =a^2 +b^2 +ab+ca+bc+c^2 =(1/2)[(a+b)^2 +(b+c)^2 +(c+a)^2 ] =(1/2)[4×9999+4×99+4×999] =2[9999+999+99] =18[1111+111+11] =18×1233)=9×2466 =22194 . ( option A)](Q20500.png)
| ||
Question and Answers Forum | ||
Question Number 20488 by xing last updated on 27/Aug/17 | ||
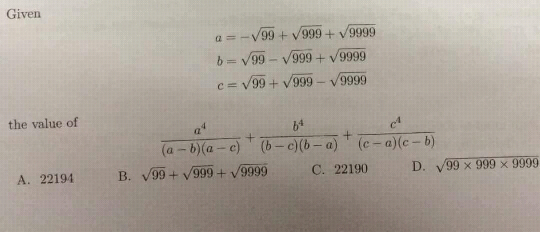 | ||
Commented by ajfour last updated on 27/Aug/17 | ||
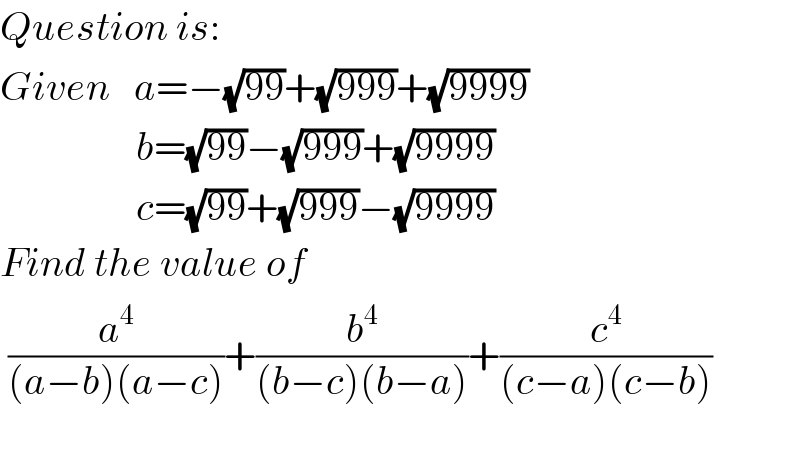 | ||
Answered by ajfour last updated on 27/Aug/17 | ||
![Let a=pc , b=qc ; then (a^4 /((a−b)(a−c)))+(b^4 /((b−c)(b−a)))+(c^4 /((c−a)(c−b))) =((p^4 c^4 )/(c^2 (p−q)(p−1)))+((q^4 c^4 )/(c^2 (q−1)(q−p))) +(c^4 /(c^2 (1−p)(1−q))) =(c^2 /((p−q)))[(p^4 /(p−1))−(q^4 /(q−1))+((p−q)/((1−p)(1−q)))] =(c^2 /((p−q)))[((p^4 q−p^4 −pq^4 +q^4 +p−q)/((1−p)(1−q)))] =(c^2 /((p−q)))[((pq(p^3 −q^3 )−(p^4 −q^4 )+(p−q))/((1−p)(1−q)))] =c^2 [((pq(p^2 +q^2 +pq)−(p^2 +q^2 )(p+q)+1)/((1−p)(1−q)))] =c^2 [(((p^2 +q^2 )(pq−p−q)+p^2 q^2 +1)/((1−p)(1−q)))] =c^2 [(((p^2 +q^2 )(p−1)(q−1)−p^2 −q^2 +p^2 q^2 +1)/((1−p)(1−q)))] =c^2 [(((p^2 +q^2 )(p−1)(q−1)+(p^2 −1)(q^2 −1))/((1−p)(1−q)))] =c^2 [p^2 +q^2 +(p+1)(q+1)] =c^2 [p^2 +q^2 +pq+p+q+1] =a^2 +b^2 +ab+ca+bc+c^2 =(1/2)[(a+b)^2 +(b+c)^2 +(c+a)^2 ] =(1/2)[4×9999+4×99+4×999] =2[9999+999+99] =18[1111+111+11] =18×1233)=9×2466 =22194 . ( option A)](Q20500.png) | ||
| ||