
Question and Answers Forum
Question Number 21394 by mondodotto@gmail.com last updated on 22/Sep/17

Answered by mrW1 last updated on 22/Sep/17
![t=(√(2x+1)) x=((t^2 −1)/2) dx=tdt ∫x(√(2x+1)) dx=∫((t^2 −1)/2)×t×tdt =(1/2)∫(t^4 −t^2 )dt =(t^5 /(10))−(t^3 /6)+C =(t^3 /2)((t^2 /5)−(1/3))+C =(((2x+1)(√(2x+1)))/2)[((2x+1)/5)−(1/3)]+C =(((3x−1)(2x+1)(√(2x+1)))/(15))+C](Q21396.png)
Answered by sma3l2996 last updated on 22/Sep/17
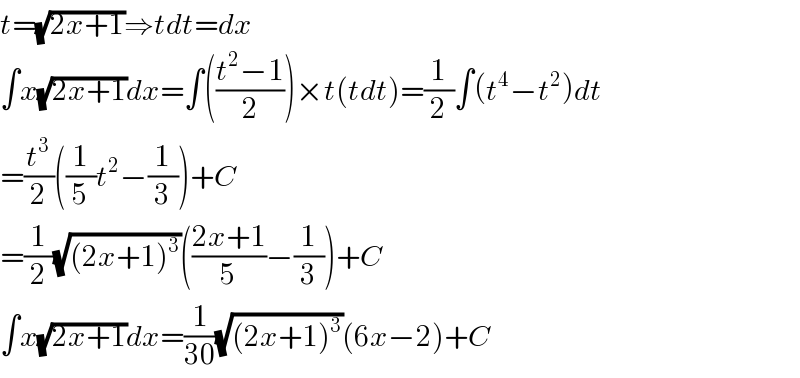
Commented by edward last updated on 23/Sep/17
| ||
Question and Answers Forum | ||
Question Number 21394 by mondodotto@gmail.com last updated on 22/Sep/17 | ||
 | ||
Answered by mrW1 last updated on 22/Sep/17 | ||
![t=(√(2x+1)) x=((t^2 −1)/2) dx=tdt ∫x(√(2x+1)) dx=∫((t^2 −1)/2)×t×tdt =(1/2)∫(t^4 −t^2 )dt =(t^5 /(10))−(t^3 /6)+C =(t^3 /2)((t^2 /5)−(1/3))+C =(((2x+1)(√(2x+1)))/2)[((2x+1)/5)−(1/3)]+C =(((3x−1)(2x+1)(√(2x+1)))/(15))+C](Q21396.png) | ||
| ||
Answered by sma3l2996 last updated on 22/Sep/17 | ||
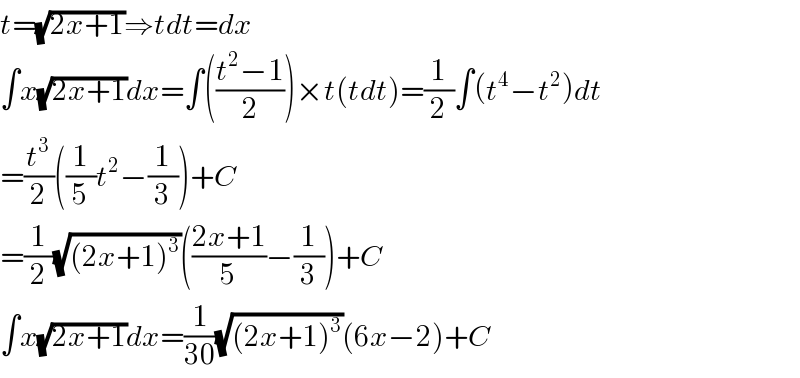 | ||
| ||
Commented by edward last updated on 23/Sep/17 | ||
 | ||