
Question and Answers Forum
Question Number 21503 by mondodotto@gmail.com last updated on 25/Sep/17

Answered by $@ty@m last updated on 26/Sep/17
![Let 4x^2 =t ⇒8xdx=dt Change of limits: As x→4, t→64 As x→y, t→4y^2 I=∫_(64) ^(4y^2 ) (√(1−t))(dt/8) ATQ, 0=(1/8)∫_(64) ^(4y^2 ) (√(1−t))dt 0=[((2(1−t)^(3/2) )/3)]_(64) ^(4y^2 ) (1−4y^2 )^(3/2) −(−63)^(3/2) =0 (1−4y^2 )^(3/2) =(−63)^(3/2) 1−4y^2 =−63 4y^2 =64 y=±4](Q21511.png)
Commented by mrW1 last updated on 26/Sep/17
![1−4x^2 ≥0 ⇒x^2 ≤(1/4) ⇒−(1/2)≤x≤(1/2) i.e. function x(√(1−4x^2 )) is defined only for x∈[−(1/2),(1/2)].](Q21515.png)
Commented by $@ty@m last updated on 26/Sep/17
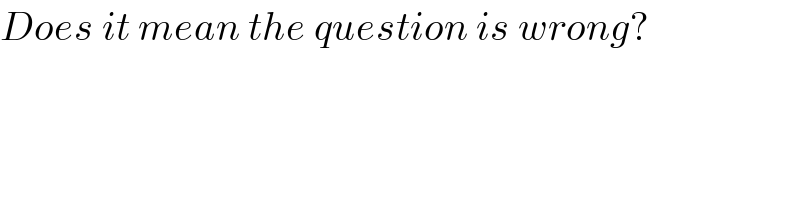
Commented by mrW1 last updated on 26/Sep/17

Commented by abwayh last updated on 26/Sep/17
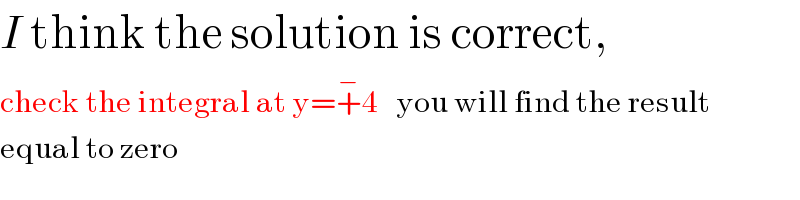
Commented by mrW1 last updated on 26/Sep/17
![as for the definition of definite integral ∫_a ^( b) f(x), the function f(x) must be continuous on the interval [a, b]. but x(√(1−4x^2 )) is not defined on [−4, −(1/2)] and [(1/2), 4]. so ∫_(−4) ^( −(1/2)) x(√(1−4x^2 )) dx and ∫_(1/2) ^( 4) x(√(1−4x^2 )) dx are also not defined. ∫_(−4) ^( 4) x(√(1−4x^2 )) dx is also not defined, since ∫_(−4) ^( 4) x(√(1−4x^2 )) dx=∫_(−4) ^( −(1/2)) x(√(1−4x^2 )) dx +∫_(−(1/2)) ^( (1/2)) x(√(1−4x^2 )) dx+ ∫_(1/2) ^( 4) x(√(1−4x^2 )) dx](Q21539.png)
Commented by abwayh last updated on 26/Sep/17

