Question and Answers Forum
Question Number 23390 by ajfour last updated on 29/Oct/17

Commented by ajfour last updated on 31/Oct/17

Commented by ajfour last updated on 31/Oct/17

Answered by mrW1 last updated on 30/Oct/17

Commented by mrW1 last updated on 31/Oct/17
![Point 1=COM of ring M Point 2=COM of rod (spoke) m x_1 =Rθ y_1 =R x_2 =x_1 +(R/2) sin θ=(R/2)(2θ+sin θ) y_2 =y_1 +(R/2) cos θ=(R/2)(2+cos θ) ω=(dθ/dt) v_(x1) =(dx_1 /dt)=R(dθ/dt)=Rω v_(y1) =(dy_1 /dt)=0 v_(x2) =(dx_2 /dt)=(R/2)(2+cos θ)ω v_(y2) =(dy_2 /dt)=−(R/2) sin θ ω KE_1 =(1/2)M(v_(x1) ^2 +v_(y1) ^2 )+(1/2)I_1 ω^2 =(1/2)MR^2 ω^2 +(1/2)MR^2 ω^2 =MR^2 ω^2 KE_2 =(1/2)m(v_(x2) ^2 +v_(y2) ^2 )+(1/2)I_2 ω^2 =((mR^2 ω^2 )/8)(5+4cos θ)+((mR^2 ω^2 )/(24)) =((mR^2 ω^2 )/6)(4+3cos θ) KE_1 +KE_2 =((mgR)/2)(1−cos θ) MR^2 ω^2 +((mR^2 ω^2 )/6)(4+3cos θ)=((mgR)/2)(1−cos θ) [6M+4m+3mcos θ]Rω^2 =3mg(1−cos θ) ω^2 =(g/R)×((1−cos θ)/(((6M+4m)/(3m))+cos θ))=(g/R)×((2 sin^2 (θ/2))/(((6M+4m)/(3m))+1−2sin^2 (θ/2))) ω^2 =(g/R)×((sin^2 (θ/2))/(((6M+7m)/(6m))−sin^2 (θ/2))) ω^2 =(g/R)×((sin^2 (θ/2))/(a^2 −sin^2 (θ/2))), with a^2 =((6M+7m)/(6m))=(M/m)+(7/6)>1 ⇒ω=(√(g/R))×((sin (θ/2))/(√(a^2 −sin^2 (θ/2))))=(dθ/dt) ⇒((√(a^2 −sin^2 (θ/2)))/(sin (θ/2))) dθ=(√(g/R)) dt ⇒(√(g/R))∫_0 ^( t) dt=∫_0 ^( θ) ((√(a^2 −sin^2 (θ/2)))/(sin (θ/2))) dθ ⇒t=(√(R/g))∫_0 ^( θ) ((√(a^2 −sin^2 (θ/2)))/(sin (θ/2))) dθ t=2(√(R/g))∫_0 ^( θ) ((√(a^2 −sin^2 (θ/2)))/(sin (θ/2))) d(θ/2) t=2(√(R/g))∫_0 ^( ϕ) ((√(a^2 −sin^2 ϕ))/(sin ϕ)) dϕ, with ϕ=(θ/2) the time which is needed for a cycle is T=2(√(R/g))∫_0 ^( π) ((√(a^2 −sin^2 ϕ))/(sin ϕ)) dϕ F(ϕ)=∫^ ((√(a^2 −sin^2 ϕ))/(sin ϕ)) dϕ =−(1/2)[a×ln ∣(((√(a^2 −sin^2 ϕ))+a ∣cos ϕ∣)/((√(a^2 −sin^2 ϕ))−a ∣cos ϕ∣))∣+ln ∣(((√(a^2 −sin^2 ϕ))−∣cos ϕ∣)/((√(a^2 −sin^2 ϕ))+∣cos ϕ∣))∣]+C =−(1/2)[a×ln ∣(((√((a^2 −1)tan^2 ϕ+a^2 ))+a)/((√((a^2 −1)tan^2 ϕ+a^2 ))−a))∣+ln ∣(((√((a^2 −1)tan^2 ϕ+a^2 ))−1)/((√((a^2 −1)tan^2 ϕ+a^2 ))+1))∣]+C ...... I can not continue due to problems with this integral at ϕ=0 and ϕ=π. what is wrong above ???](Q23440.png)
Commented by ajfour last updated on 31/Oct/17

Commented by mrW1 last updated on 31/Oct/17

Commented by mrW1 last updated on 31/Oct/17

Commented by mrW1 last updated on 31/Oct/17
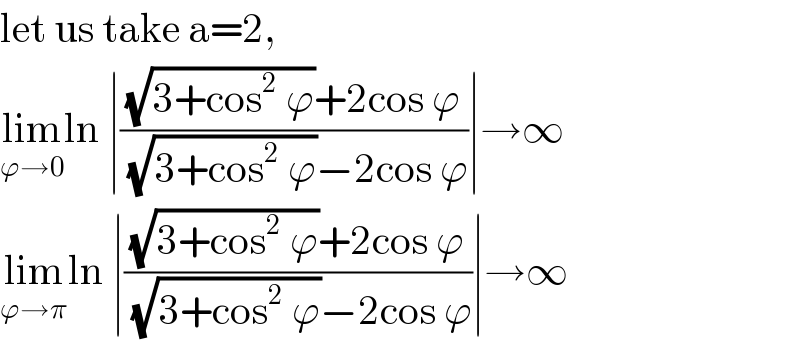
Commented by ajfour last updated on 31/Oct/17
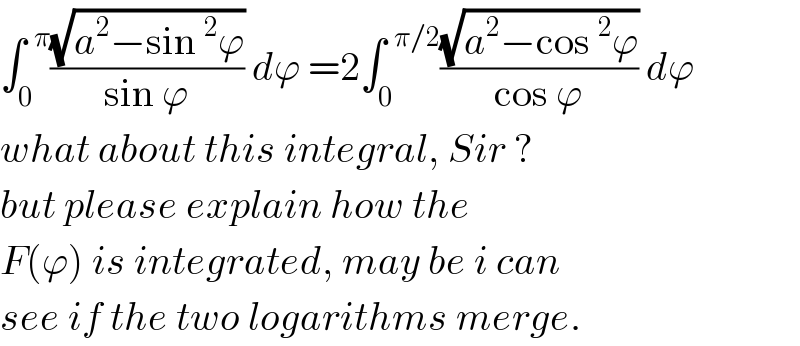
Commented by mrW1 last updated on 31/Oct/17

Commented by ajfour last updated on 31/Oct/17