Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 27997 by ajfour last updated on 18/Jan/18

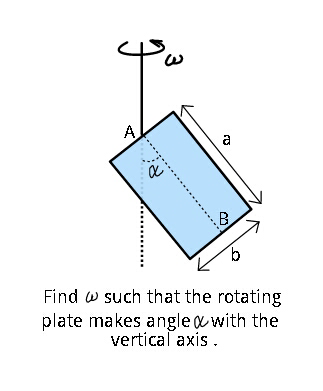
Commented by mrW2 last updated on 18/Jan/18

$$\omega =\sqrt{\frac{3g}{2a\cos \alpha }}$$

Commented by ajfour last updated on 18/Jan/18

$$yessir,pleaseseemysolution$$$$whenipost.Beforehandcani$$$$havesomeworkingstepstothis$$$$answer..$$

Commented by ajfour last updated on 18/Jan/18

$$Whatisthemaximumvalueof$$$$\omega forwhichtheplatecanstayin$$$$verticalplane?$$

Answered by mrW2 last updated on 18/Jan/18

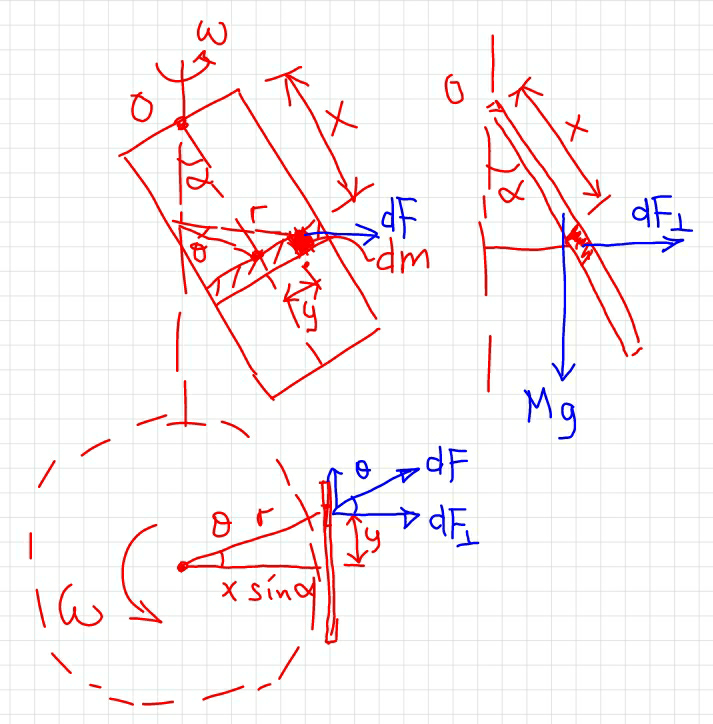
Commented by mrW2 last updated on 18/Jan/18

$$\rho =\frac{M}{ab}$$$$dm=\rho dydx$$$$dF=r{\omega }^{2}dm$$$${dF}_{\mathrm{\perp }}=\cos \theta dF=\rho {\omega }^{2}r\cos \theta dydx$$$$r^2={\left(x\sin \alpha \right)}^2+y^2$$$$r\cos \theta =x\sin \alpha$$$$\Rightarrow {dF}_{\mathrm{\perp }}=\rho {\omega }^2\sin \alpha xdydx$$$$\frac{Mga\sin \alpha }{2}=\int x\cos \alpha {dF}_{\mathrm{\perp }}=\rho {\omega }^2\sin \alpha \cos \alpha {\int }_0^a{\int }_{-\frac{b}{2}}^{\frac{b}{2}}{x}^{2}dydx$$$$\frac{Mga\sin \alpha }{2}=\rho {\omega }^2\sin \alpha \cos \alpha \frac{a^{3}b}{3}$$$$\frac{Mg}{2}=\rho {\omega }^2\cos \alpha \frac{a^{2}b}{3}$$$$\frac{g}{2}={\omega }^2\cos \alpha \frac{a}{3}$$$$\Rightarrow \omega =\sqrt{\frac{3g}{2a\cos \alpha }}$$$$$$$$for\alpha =0$$$$\Rightarrow {\omega }_{max}=\sqrt{\frac{3g}{2a}}$$

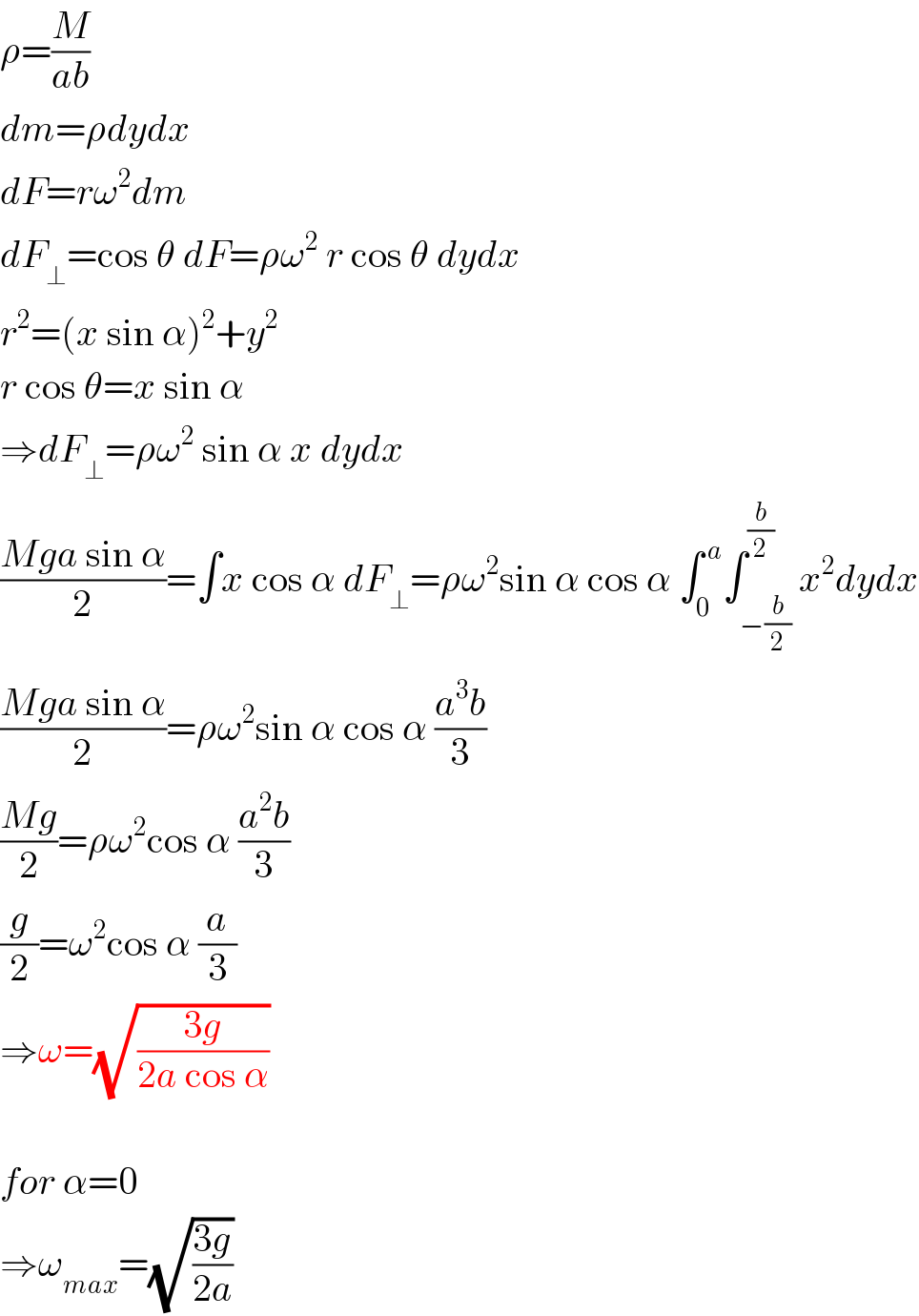
Commented by ajfour last updated on 18/Jan/18

Thank you too much Sir. I enjoyed thoroughly following the solution Sir.

Terms of Service

Privacy Policy

Contact: info@tinkutara.com