
Question and Answers Forum
Question Number 35635 by ajfour last updated on 21/May/18

Commented by ajfour last updated on 21/May/18
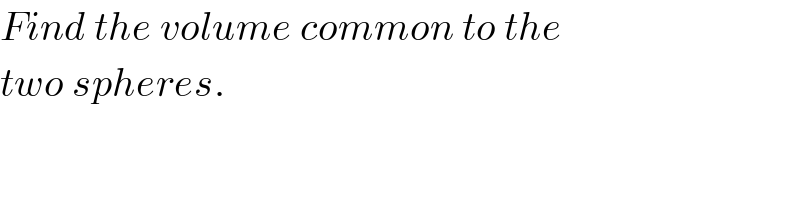
Answered by ajfour last updated on 21/May/18
![Let centre of lower sphere be origin and line joining the centres, the z-axis. eqn. of lower sphere is z^2 =R^2 −(x^2 +y^2 ) eqn. of upper sphere is (z−d)^2 =r^2 −(x^2 +y^2 ) equating the two we get z_c ^2 −(z_c −d)^2 = R^2 −r^2 or (2z_c −d)d=R^2 −r^2 ...(i) Required volume V_c is V_c =∫_(d−r) ^( z_c ) π[r^2 −(d−z)^2 ]dz + ∫_z_c ^( R) π(R^2 −z^2 )dz =π{[r^2 z+(((d−z)^3 )/3)]_(d−r) ^z_c +(R^2 z−(z^3 /3))_z_c ^R } =π[r^2 z_c +(((d−z_c )^3 )/3)−r^2 (d−r)−(r^3 /3)] +π[R^3 −(R^3 /3)−R^2 z_c +(z_c ^3 /3)] V_c =π[((2(R^3 +r^3 ))/3)−(R^2 −r^2 )z_c −r^2 d +(d^3 /3)−d^2 z_c +z_c ^2 d ] ...(ii) Using (i) : V_c = π[((2(R^3 +r^3 ))/3)+(d^3 /3)−r^2 d−2z_c ^2 d+z_c ^2 d] V_c =π[((2(R^3 +r^3 ))/3)+(d^3 /3)−r^2 d−(((d^2 +R^2 −r^2 )^2 )/(4d))] .](Q35638.png)
Commented by ajfour last updated on 21/May/18
![If d=R+r then V_c =0 lets check: V_c ∣_(d=R+r) =π[((2(R^3 +r^3 ))/3)+(((R+r)^3 )/3) −r^2 (R+r)−(([(R+r)^2 +R^2 −r^2 ]^2 )/(4(R+r)))] V_c =π[(2/3)(R^3 +r^3 )+(((R+r)^3 )/3) −r^2 (R+r)−(((R+r)^3 )/4)−(((R+r)(R−r)^2 )/4) −(((R+r)^2 (R−r))/2) ] =π[((2/3)+(1/3)−(1/4)−(1/4)−(1/2))R^3 +(0+1−(3/4)−(1/4)+(1/2))R^2 r +(0+1−1−(3/4)+(1/4)+(1/2))r^2 R +(+(2/3)+(1/3)−1−(1/4)−(1/4)+(1/2))r^3 ] = 0 (indeed) •](Q35641.png)
| ||
Question and Answers Forum | ||
Question Number 35635 by ajfour last updated on 21/May/18 | ||
 | ||
Commented by ajfour last updated on 21/May/18 | ||
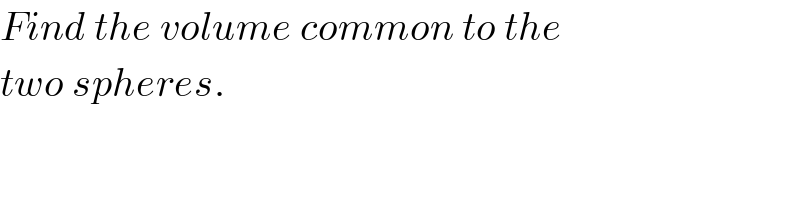 | ||
Answered by ajfour last updated on 21/May/18 | ||
![Let centre of lower sphere be origin and line joining the centres, the z-axis. eqn. of lower sphere is z^2 =R^2 −(x^2 +y^2 ) eqn. of upper sphere is (z−d)^2 =r^2 −(x^2 +y^2 ) equating the two we get z_c ^2 −(z_c −d)^2 = R^2 −r^2 or (2z_c −d)d=R^2 −r^2 ...(i) Required volume V_c is V_c =∫_(d−r) ^( z_c ) π[r^2 −(d−z)^2 ]dz + ∫_z_c ^( R) π(R^2 −z^2 )dz =π{[r^2 z+(((d−z)^3 )/3)]_(d−r) ^z_c +(R^2 z−(z^3 /3))_z_c ^R } =π[r^2 z_c +(((d−z_c )^3 )/3)−r^2 (d−r)−(r^3 /3)] +π[R^3 −(R^3 /3)−R^2 z_c +(z_c ^3 /3)] V_c =π[((2(R^3 +r^3 ))/3)−(R^2 −r^2 )z_c −r^2 d +(d^3 /3)−d^2 z_c +z_c ^2 d ] ...(ii) Using (i) : V_c = π[((2(R^3 +r^3 ))/3)+(d^3 /3)−r^2 d−2z_c ^2 d+z_c ^2 d] V_c =π[((2(R^3 +r^3 ))/3)+(d^3 /3)−r^2 d−(((d^2 +R^2 −r^2 )^2 )/(4d))] .](Q35638.png) | ||
| ||
Commented by ajfour last updated on 21/May/18 | ||
![If d=R+r then V_c =0 lets check: V_c ∣_(d=R+r) =π[((2(R^3 +r^3 ))/3)+(((R+r)^3 )/3) −r^2 (R+r)−(([(R+r)^2 +R^2 −r^2 ]^2 )/(4(R+r)))] V_c =π[(2/3)(R^3 +r^3 )+(((R+r)^3 )/3) −r^2 (R+r)−(((R+r)^3 )/4)−(((R+r)(R−r)^2 )/4) −(((R+r)^2 (R−r))/2) ] =π[((2/3)+(1/3)−(1/4)−(1/4)−(1/2))R^3 +(0+1−(3/4)−(1/4)+(1/2))R^2 r +(0+1−1−(3/4)+(1/4)+(1/2))r^2 R +(+(2/3)+(1/3)−1−(1/4)−(1/4)+(1/2))r^3 ] = 0 (indeed) •](Q35641.png) | ||