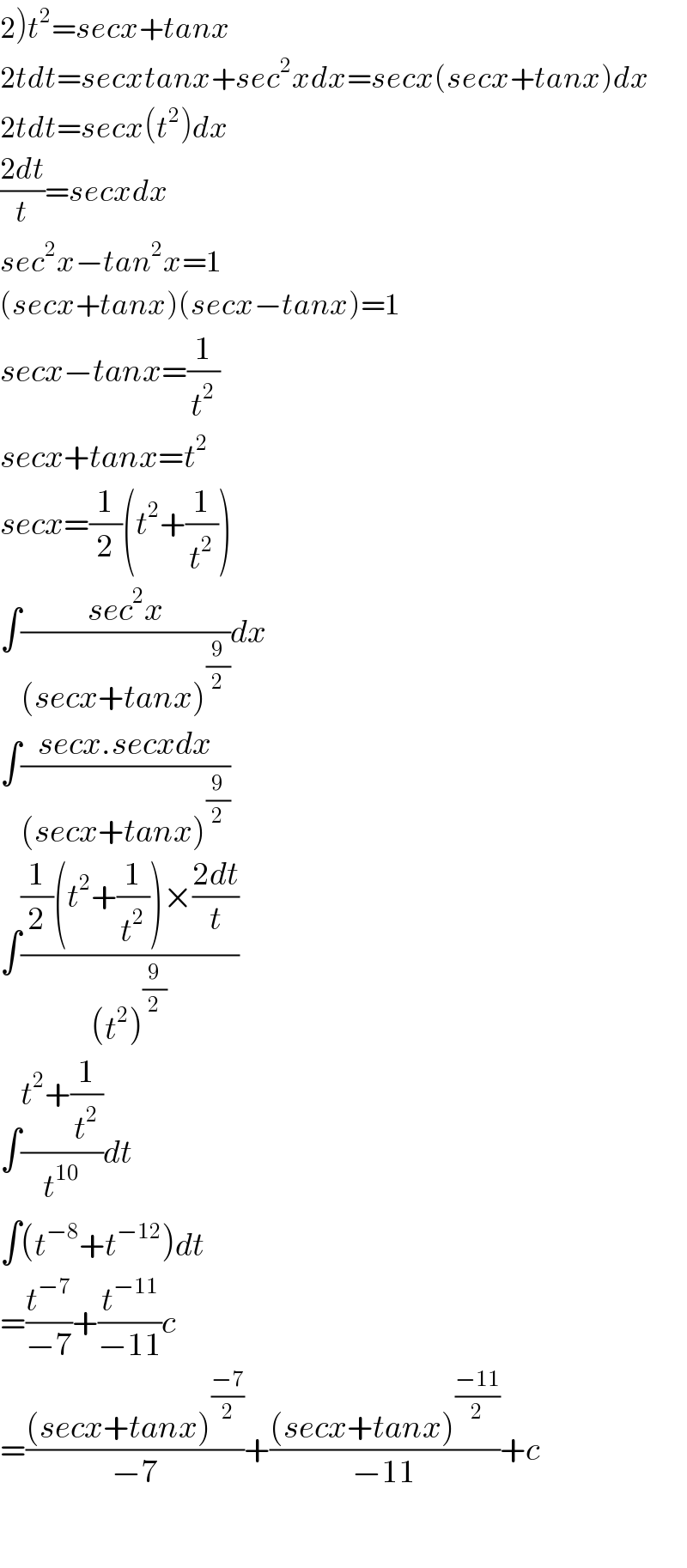Question and Answers Forum
Question Number 41436 by Raj Singh last updated on 07/Aug/18

Answered by rahul 19 last updated on 07/Aug/18

Answered by MJS last updated on 07/Aug/18
![∫(dx/(x^4 +8x^2 +9))=∫(dx/((x^2 +4−(√7))(x^2 +4+(√7))))= ((√7)/(14))∫(dx/(x^2 +4−(√7)))−((√7)/(14))∫(dx/(x^2 +4+(√7)))= [∫(dt/(t^2 +a))=((√a)/a)arctan ((x(√a))/a)] =(((7(√2)+(√(14)))/(84)))arctan ((((√(14))+(√2))/6)x) −(((7(√2)−(√(14)))/(84)))arctan ((((√(14))−(√2))/6)x) +4c](Q41438.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Aug/18
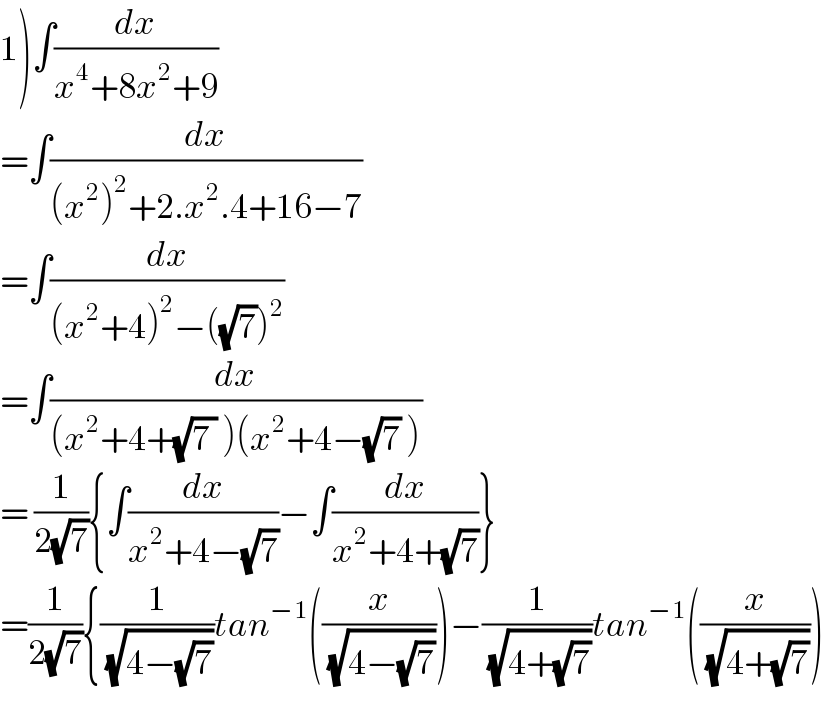
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Aug/18