Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 45885 by Meritguide1234 last updated on 17/Oct/18

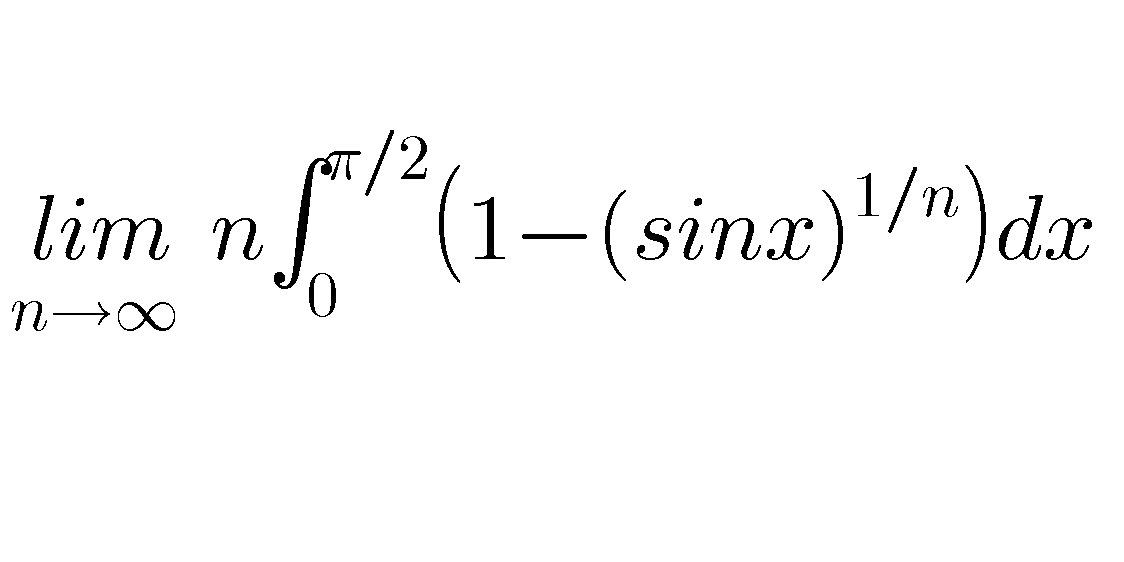
Commented by maxmathsup by imad last updated on 18/Oct/18

$l e t A_{n} = \int_{0}^{\frac{π}{2}} n (1 - {(s i n x)}^{\frac{1}{n}}) d x = \int_{0}^{\frac{π}{2}} f_{n} (x) d x w i t h f_{n} (x) = n (1 - ({s i n x}^{\frac{1}{n}}))$ $b u t w e h a v e {(s i n x)}^{\frac{1}{n}} = e^{\frac{1}{n} l n (s i n x)} = 1 + \frac{l n (s i n x)}{n} + o (\frac{1}{n}) \Rightarrow$ $1 - e^{\frac{1}{n} l n (s i n x)} = - \frac{l n (s i n x)}{n} + o (\frac{1}{n}) \Rightarrow n (1 - e^{\frac{l n (s i n x)}{n}}) = - l n (s i n x) + o (1) \Rightarrow$ $f_{n} (x) = - l n (s i n x) + o (1) \Rightarrow {l i m}_{n \to + \infty} A_{n} = \int_{0}^{\frac{π}{2}} - l n (s i n x) d x$ $= - (- \frac{π}{2} l n (2)) = \frac{π}{2} l n (2) .$
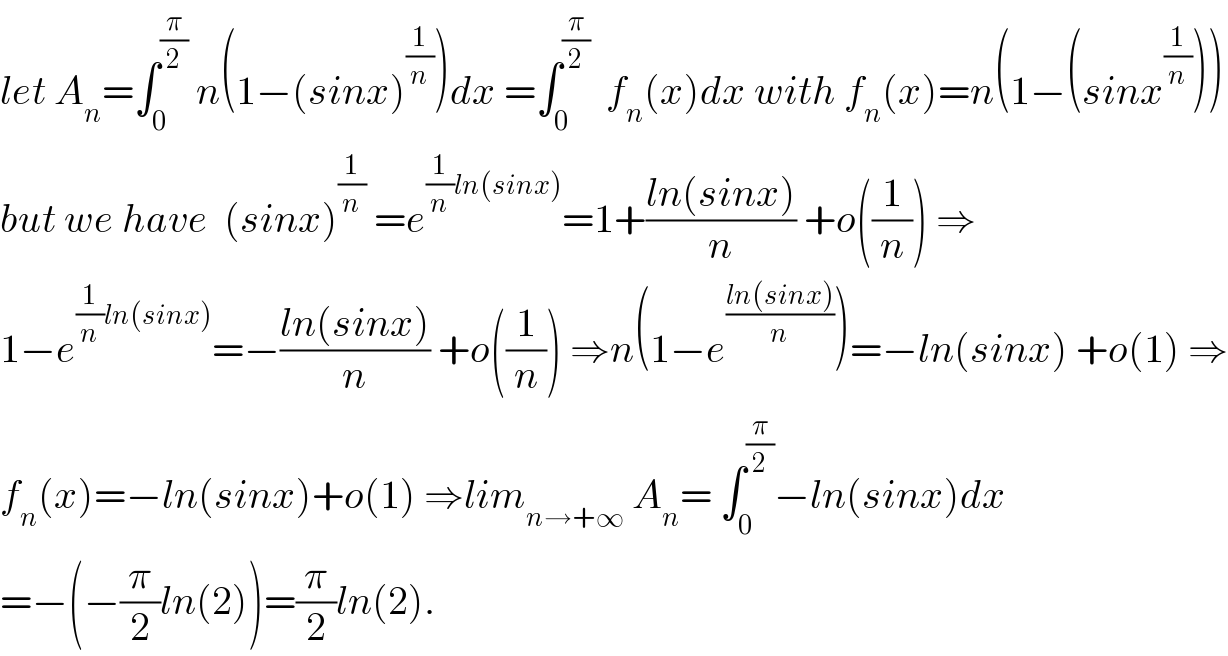
Commented by Meritguide1234 last updated on 19/Oct/18

$n i c e a p p r o a c h$
Commented by maxmathsup by imad last updated on 20/Oct/18

$t h a n k y o u s i r .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 17/Oct/18
	$lim_(n→∞) n∫_0 ^(π/2) {1−(sinx)^(1/n) }dx lim_(n→∞) n[∣x∣_0 ^(π/2) −∫_0 ^(π/2) sin^(2p−1) xcoz^(2q−1) x dx] here 2p−1=(1/n) 2p=1+(1/n) p=((n+1)/(2n)) 2q−1=0 q=(1/2) using gamma beta function formula ∫_0 ^(π/2) sin^(2p−1) xcos^(2a−1) xdx=((⌈(p)⌈(q))/(2⌈(p+q))) lim_(n→∞) n[(π/2)−((⌈(p)⌈(q))/(2⌈(p+q)))] lim_(n→∞) n[(π/2)−((⌈(((n+1)/(2n)))⌈((1/2)))/(2⌈(((n+1)/(2n))+(1/2))))] lim_(n→∞) n[(π/2)−((⌈(1+((1−n)/(2n)))×(√π))/(2⌈(1+((n+1)/(2n))−(1/2)))) ] lim_(n→∞) n[(π/2)−(((√π) ×⌈(1+((1−n)/(2n))))/(2⌈(1+(1/(2n)))))]$
	$\lim_{n \to \infty} n \int_{0}^{\frac{π}{2}} {1 - {(s i n x)}^{\frac{1}{n}}} d x$ $\lim_{n \to \infty} n [∣ x ∣_{0}^{\frac{π}{2}} - \int_{0}^{\frac{π}{2}} {s i n}^{2 p - 1} {x c o z}^{2 q - 1} x d x]$ $h e r e 2 p - 1 = \frac{1}{n} 2 p = 1 + \frac{1}{n} p = \frac{n + 1}{2 n}$ $2 q - 1 = 0 q = \frac{1}{2} u s i n g g a m m a b e t a f u n c t i o n$ $f o r m u l a \int_{0}^{\frac{π}{2}} {s i n}^{2 p - 1} {x c o s}^{2 a - 1} x d x = \frac{⌈ (p) ⌈ (q)}{2 ⌈ (p + q)}$ $\lim_{n \to \infty} n [\frac{π}{2} - \frac{⌈ (p) ⌈ (q)}{2 ⌈ (p + q)}]$ $\lim_{n \to \infty} n [\frac{π}{2} - \frac{⌈ (\frac{n + 1}{2 n}) ⌈ (\frac{1}{2})}{2 ⌈ (\frac{n + 1}{2 n} + \frac{1}{2})}]$ $\lim_{n \to \infty} n [\frac{π}{2} - \frac{⌈ (1 + \frac{1 - n}{2 n}) \times \sqrt{π}}{2 ⌈ (1 + \frac{n + 1}{2 n} - \frac{1}{2})}]$ $\lim_{n \to \infty} n [\frac{π}{2} - \frac{\sqrt{π} \times ⌈ (1 + \frac{1 - n}{2 n})}{2 ⌈ (1 + \frac{1}{2 n})}]$
	Commented by Meritguide1234 last updated on 18/Oct/18

	$n o t c o r r e c t$
	Commented by tanmay.chaudhury50@gmail.com last updated on 18/Oct/18

	$y e s i k n o w t h e r e s u l t i s y e t t o c o m e . . . w h e n n \to \infty$ $t h e r e s u l t s i s \infty$
	Commented by Meritguide1234 last updated on 18/Oct/18

	$p u t n = 1 / t . . . t h e n a n s i s (\frac{π}{2} l n 2)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum