
Question and Answers Forum
Question Number 47401 by Aditya789 last updated on 09/Nov/18

Commented by maxmathsup by imad last updated on 10/Nov/18
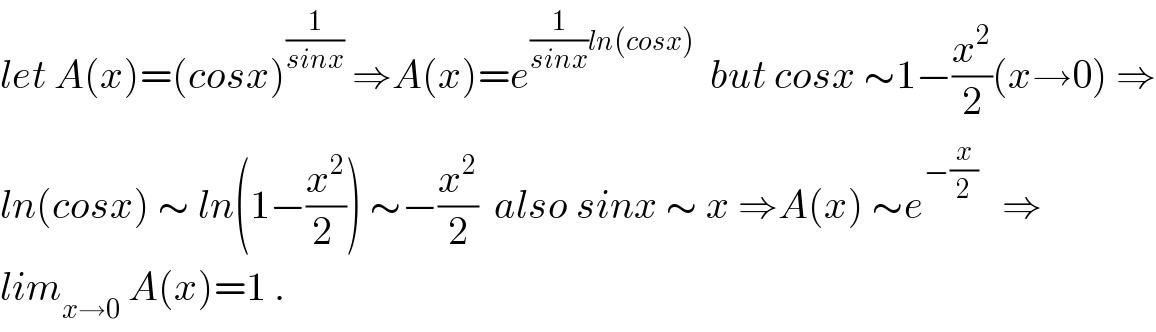
Answered by ajfour last updated on 09/Nov/18
![= lim_(x→0) [1−(1−cos x)]^(1/sin x) =lim_(x→0) {[1−2sin^2 (x/2)]^(−1/2sin^2 (x/2)) }^(−((2sin^2 (x/2))/(2sin (x/2)cos (x/2)))) = lim_(x→0) e^(−tan (x/2)) = 1 .](Q47405.png)
Answered by rahul 19 last updated on 11/Nov/18
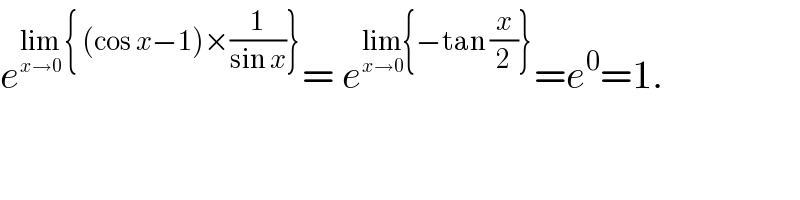
| ||
Question and Answers Forum | ||
Question Number 47401 by Aditya789 last updated on 09/Nov/18 | ||
 | ||
Commented by maxmathsup by imad last updated on 10/Nov/18 | ||
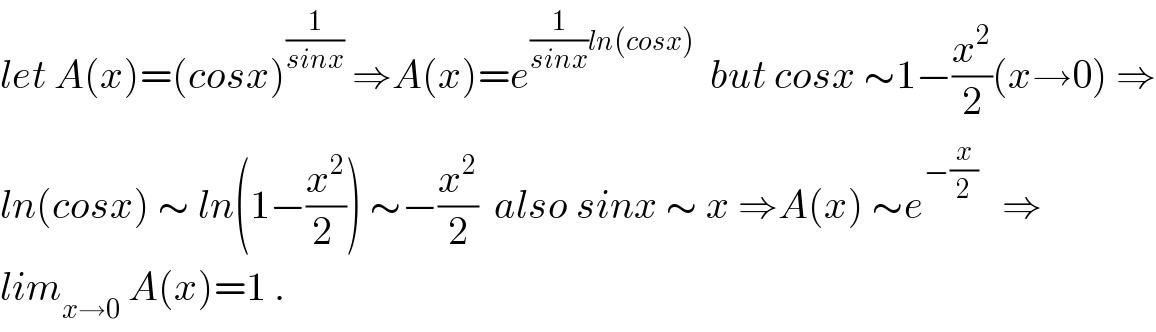 | ||
Answered by ajfour last updated on 09/Nov/18 | ||
![= lim_(x→0) [1−(1−cos x)]^(1/sin x) =lim_(x→0) {[1−2sin^2 (x/2)]^(−1/2sin^2 (x/2)) }^(−((2sin^2 (x/2))/(2sin (x/2)cos (x/2)))) = lim_(x→0) e^(−tan (x/2)) = 1 .](Q47405.png) | ||
| ||
Answered by rahul 19 last updated on 11/Nov/18 | ||
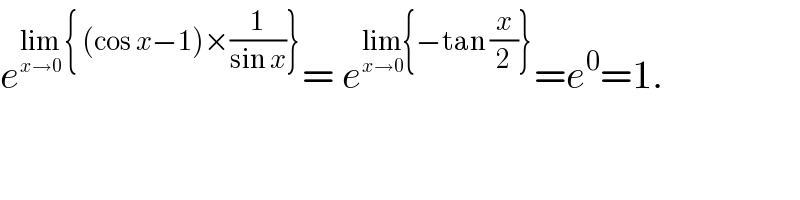 | ||
| ||