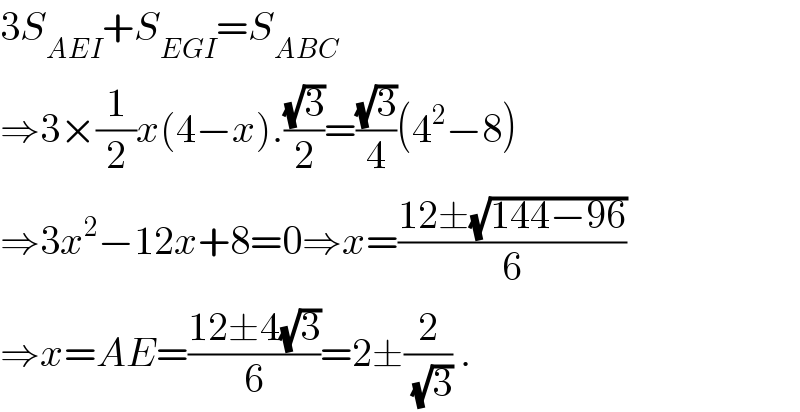Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 49530 by behi83417@gmail.com last updated on 07/Dec/18

Commented by behi83417@gmail.com last updated on 07/Dec/18

$△ a n d △ a r e e q u i l a t e r a l t r i a n g l e s .$ $A B = 4, E G = 2 \sqrt{2} [o r : A B = 6, E G = 2 \sqrt{6}]$ $\Rightarrow A E = ?, ∡ A E I = ?$
Commented by mr W last updated on 07/Dec/18

$n o t p o s s i b l e s i r!$ $E G ⩾ A B / 2 = 6 / 2 = 3$ $\Rightarrow w i t h E G = \sqrt{6} < 3 n o s o l u t i o n!$
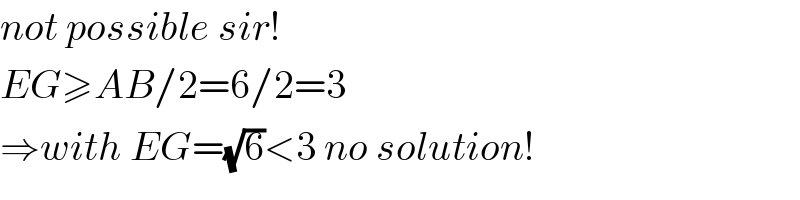
Commented by behi83417@gmail.com last updated on 07/Dec/18

$y e s s i r . y o u a r e r i g h t . v a l u e s c h a n g e d .$
	Answered by mr W last updated on 07/Dec/18

	$A E = x$ $4 = x + \frac{x}{2} + \sqrt{{(2 \sqrt{2})}^{2} - {(\frac{\sqrt{3} x}{2})}^{2}}$ $4 - \frac{3 x}{2} = \sqrt{8 - \frac{3 x^{2}}{4}}$ $8 - 3 x = \sqrt{32 - 3 x^{2}}$ $64 - 48 x + 9 x^{2} = 32 - 3 x^{2}$ $8 - 12 x + 3 x^{2} = 0$ $\Rightarrow x = \frac{6 \pm 2 \sqrt{3}}{3} = 0.845 (o r 3.155)$ $\frac{\sin θ}{x} = \frac{\sin 60 °}{2 \sqrt{2}}$ $\Rightarrow \sin θ = \frac{6 - 2 \sqrt{3}}{3} \times \frac{\sqrt{3}}{2 \times 2 \sqrt{2}} = \frac{\sqrt{6} - \sqrt{2}}{4}$ $\Rightarrow θ = \sin^{- 1} \frac{\sqrt{6} - \sqrt{2}}{4} = 15 °$ $\Rightarrow ∠ A E I = 180 ° - 60 ° - 15 ° = 105 °$
	Commented by behi83417@gmail.com last updated on 07/Dec/18

	$r i g h t a n s w e r a n d p e r f e c t w a y .$ $t h a n k y o u v e r y m u c h d e a r m a s t e r .$
	Answered by behi83417@gmail.com last updated on 07/Dec/18

	${E G}^{2} = {G B}^{2} + {E B}^{2} - 2 G B . E B . c o s 60$ ${(2 \sqrt{2})}^{2} = x^{2} + {(4 - x)}^{2} - 2 x (4 - x) . \frac{1}{2}$ $3 x^{2} - 12 x + 8 = 0 \Rightarrow x = A E = \frac{12 \pm \sqrt{144 - 96}}{6}$ $A E = \frac{12 \pm 4 \sqrt{3}}{6} = 2 \pm \frac{2}{\sqrt{3}} . [= 0.845 \lor 3.15]$ $c o s A \overset{}{E I} = \frac{{(2 \sqrt{2})}^{2} + x^{2} - {(4 - x)}^{2}}{4 \sqrt{2} x} =$ $= \frac{8 + x^{2} - x^{2} + 8 x - 16}{4 \sqrt{2} x} = \sqrt{2} (1 - \frac{1}{x}) =$ $= \sqrt{2} (1 - \frac{1}{0.845}) = - 0.259 \Rightarrow A \overset{}{E I} = 105^{∙} .$
	Answered by behi83417@gmail.com last updated on 07/Dec/18

	$3 S_{A E I} + S_{E G I} = S_{A B C}$ $\Rightarrow 3 \times \frac{1}{2} x (4 - x) . \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{4} (4^{2} - 8)$ $\Rightarrow 3 x^{2} - 12 x + 8 = 0 \Rightarrow x = \frac{12 \pm \sqrt{144 - 96}}{6}$ $\Rightarrow x = A E = \frac{12 \pm 4 \sqrt{3}}{6} = 2 \pm \frac{2}{\sqrt{3}} .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum