Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 50052 by cesar.marval.larez@gmail.com last updated on 13/Dec/18

Commented by maxmathsup by imad last updated on 13/Dec/18

$$letI=\int \frac{x^2+2x}{{(x+1)}^2}dxchangementx+1=tgive$$$$I=\int \frac{{(t-1)}^2+2(t-1)}{t^2}dt=\int \frac{t^2-2t+1+2t-2}{t^2}dt$$$$=\int \frac{t^2-1}{t^2}dt=\int dt-\int \frac{dt}{t^2}=t+\frac{1}{t}+c\Rightarrow I=x+1+\frac{1}{x+1}+c.$$

Answered by peter frank last updated on 13/Dec/18

$$4)\int \frac{1}{\mathrm{cosx}}\mathrm{dx}$$$$\mathrm{cosx}=\frac{1-{\mathrm{t}}^2}{1+{\mathrm{t}}^2}$$$$\mathrm{t}=\tan \frac{\mathrm{x}}{2}$$$$\mathrm{dx}=\frac{2\mathrm{dt}}{1+{\mathrm{t}}^2}$$$$\int \frac{2\mathrm{dt}}{1-{\mathrm{t}}^2}=\int \frac{(1-\mathrm{t})+(1+\mathrm{t})}{1-{\mathrm{t}}^2}$$$$=\ln \frac{1+\mathrm{t}}{1-\mathrm{t}}+\mathrm{B}$$$$\ln \frac{1+\tan \frac{\mathrm{x}}{2}}{1-\tan \frac{\mathrm{x}}{2}}=\ln \left[\frac{\cos \frac{\mathrm{x}}{2}+\sin \frac{\mathrm{x}}{2}}{\cos \frac{\mathrm{x}}{2}-\sin \frac{\mathrm{x}}{2}}\right]\Rightarrow \left(\mathrm{rationalise}\mathrm{denominator}\right)$$$$\ln \left[\frac{1+\sin \mathrm{x}}{\cos \mathrm{x}}\right]+\mathrm{D}$$$$\ln [\mathrm{secx}+\tan \mathrm{x}]+\mathrm{D}$$$$$$

Commented by maxmathsup by imad last updated on 13/Dec/18

$$ingeneralletdetermine\int \frac{dx}{cos(ax+b)}witha\ne 0$$$$\int \frac{dx}{cos(ax+b)}{=}_{ax+b=t}\int \frac{1}{cos\left(t\right)}\frac{dt}{a}=\frac{1}{a}ln\mid tan(\frac{t}{2}+\frac{\pi }{4})\mid +C$$$$=\frac{1}{a}ln\mid tan(\frac{ax+b}{2}+\frac{\pi }{4})\mid +C.$$

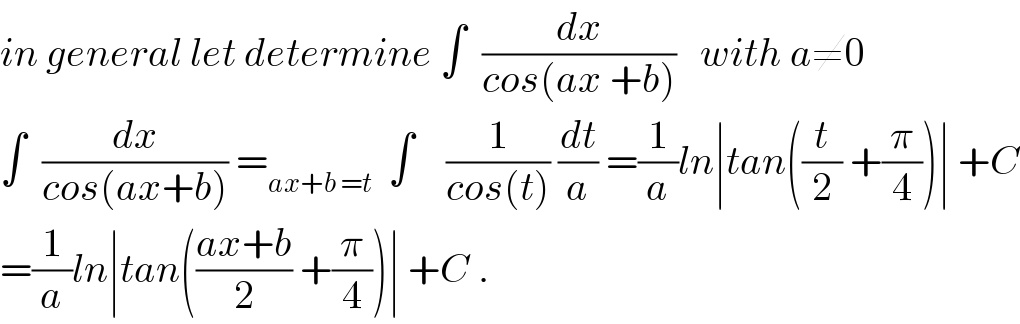
Commented by $@ty@m last updated on 13/Dec/18

$$Pl.seemycommenton$$$$Q.No.40717$$

Commented by maxmathsup by imad last updated on 13/Dec/18

$$letI=\int \frac{dx}{cosx}changementtan\left(\frac{x}{2}\right)=tgive$$$$I=\int \frac{1}{\frac{1-t^2}{1+t2}}\frac{2dt}{1+t^2}=\int \frac{2dt}{1-t^2}=\int (\frac{1}{1-t}+\frac{1}{1+t})dt$$$$=ln\mid \frac{1+t}{1-t}\mid +c=ln\mid \frac{1+tan\left(\frac{x}{2}\right)}{1-tan\left(\frac{x}{2}\right)}\mid +c=ln\mid tan(\frac{x}{2}+\frac{\pi }{4})\mid +c.$$

Answered by afachri last updated on 13/Dec/18

$$\left(1\right)\int \frac{x^2+2x}{{(x+1)}^2}dx=\int \frac{x^2+2x+1-1}{{(x+1)}^2}dx$$$$=\int \frac{{(x+1)}^2-1}{{(x+1)}^2}dx=\int \frac{{(x+1)}^2}{{(x+1)}^2}-\frac{1}{{(x+1)}^2}dx$$$$=\int 1-\frac{1}{{(x+1)}^2}dx$$$$\mathrm{first}:$$$$\int \frac{1}{{(x+1)}^2}dx\Rightarrow \mathrm{let}u=x+1$$$$du=dx$$$$\mathrm{equation}\mathrm{will}\mathrm{be}$$$$\int \frac{1}{u^2}du=\int u^{-2}du=-u^{-1}$$$$=-\frac{1}{(x+1)}$$$$\therefore \int 1-\frac{1}{{(x+1)}^2}dx=x+\frac{1}{(x+1)}+C$$

Answered by Joel578 last updated on 13/Dec/18

$$2)$$$$I=\int e^{3\cos 2x}.\sin 2xdx$$$$u=\cos 2x\to du=-2\sin 2xdx$$$$$$$$\Rightarrow I=-\frac{1}{2}\int e^{3u}du$$$$=-\frac{1}{2}(\frac{1}{3}{e}^{3u}+C)$$$$=-\frac{1}{6}{e}^{3\cos 2x}+C$$

Answered by Joel578 last updated on 14/Dec/18

$$3)$$$$I=\int \frac{dx}{e^x+1}$$$$u=e^x+1\to du=e^{x}dx$$$$dx=\frac{du}{u-1}$$$$I=\int \frac{1}{u}\left(\frac{du}{u-1}\right)=\int (\frac{-1}{u}+\frac{1}{u-1})du$$$$=-\ln \mid u\mid +\ln \mid u-1\mid +C$$$$=-\ln \mid e^x+1\mid +\ln \mid e^x\mid +C$$$$=x-\ln \mid e^x+1\mid +C$$

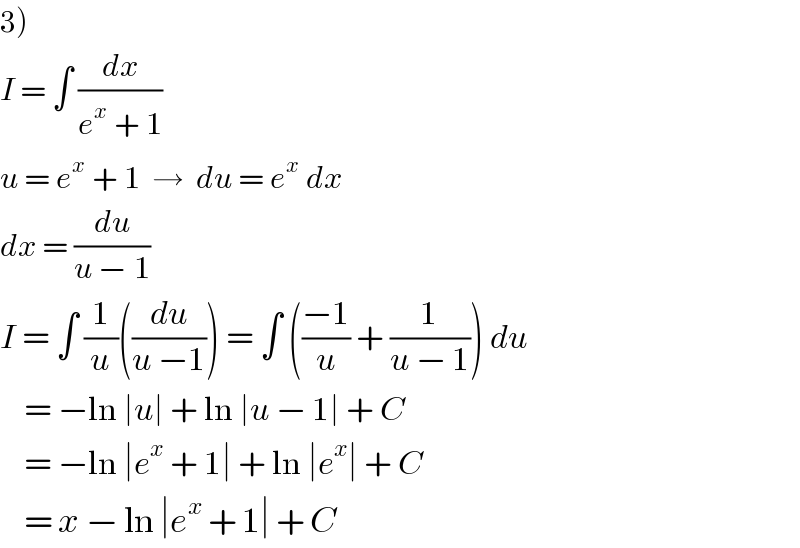
Commented by cesar.marval.larez@gmail.com last updated on 13/Dec/18

$$thankueveryone$$

Commented by afachri last updated on 14/Dec/18

Commented by Joel578 last updated on 14/Dec/18

$$thankyouforcorrection$$

Commented by afachri last updated on 24/Dec/18

$$\mathrm{your}\mathrm{welcome}\mathrm{Sir}$$

Answered by peter frank last updated on 13/Dec/18

$$3)\mathrm{t}={\mathrm{e}}^{\mathrm{x}}+1\Rightarrow {\mathrm{e}}^{\mathrm{x}}=\mathrm{t}-1$$$$\mathrm{dt}={\mathrm{e}}^{\mathrm{x}}\mathrm{dx}\Rightarrow \mathrm{dx}=\frac{\mathrm{dt}}{{\mathrm{e}}^{\mathrm{x}}}$$$$\int \frac{1}{\mathrm{t}}\frac{\mathrm{dt}}{\mathrm{t}-1}=\int \frac{-\mathrm{t}+1+\mathrm{t}}{\mathrm{t}(\mathrm{t}-1)}$$$$-\mathrm{lnt}+\ln (\mathrm{t}-1)+\mathrm{D}$$$$-\ln \left({\mathrm{e}}^{\mathrm{x}}\right)+\ln ({\mathrm{e}}^{\mathrm{x}}-1)+\mathrm{D}$$$$$$$$$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com