Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 51353 by behi83417@gmail.com last updated on 26/Dec/18

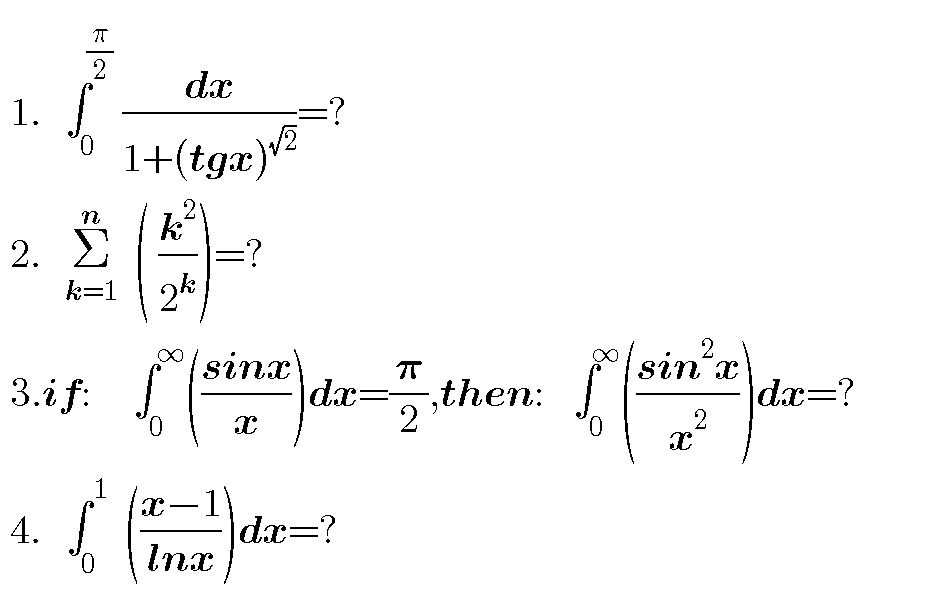
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Dec/18

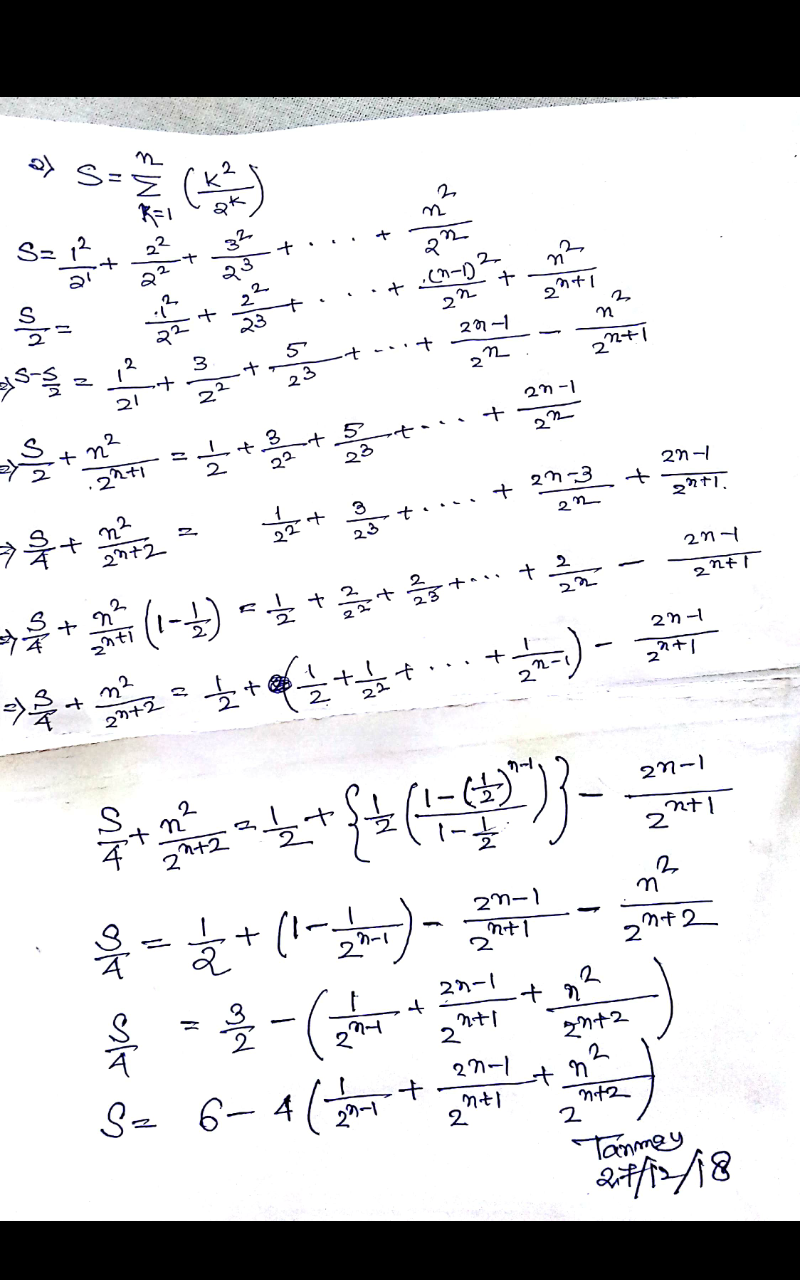
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18

$$1)I={\int }_0^{\frac{\pi }{2}}\frac{\sqrt{cosx}}{\sqrt{cosx}+\sqrt{sinx}}dx$$$$I={\int }_0^{\frac{\pi }{2}}\frac{\sqrt{cos(\frac{\pi }{2}-x)}}{\sqrt{cos(\frac{\pi }{2}-x)}+\sqrt{sin(\frac{\pi }{2}-x)}}dx$$$$2I={\int }_0^{\frac{\pi }{2}}\frac{\sqrt{cosx}+\sqrt{sinx}}{\sqrt{sinx}+\sqrt{cosx}}dx$$$$2I=\mid x{\mid }_0^{\frac{\pi }{2}}=\frac{\pi }{2}soI=\frac{\pi }{4}$$

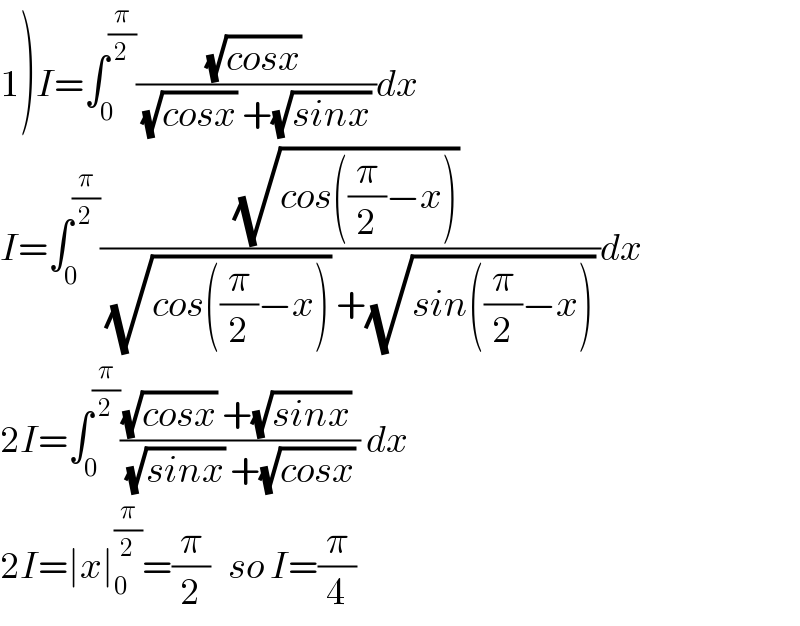
Commented by behi83417@gmail.com last updated on 26/Dec/18

$$thankalotsirtanmay.$$$$butthepoweris:\sqrt{2}...i.e:{\left(tgx\right)}^{\sqrt{2}}$$

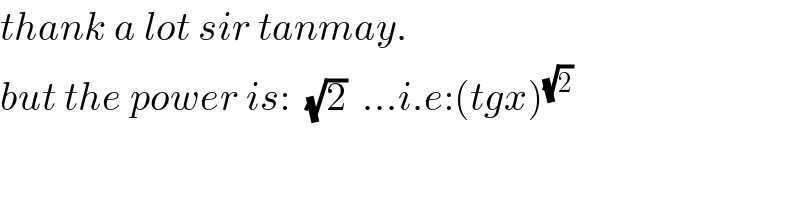
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18

$$itistheanswerof{\int }_0^{\frac{\pi }{2}}\frac{dx}{1+\sqrt{tanx}}butnot{\int }_0^{\frac{\pi }{2}}\frac{dx}{1+{\left(tanx\right)}^{\sqrt{2}}}$$$$plswait..sirletmethink...$$

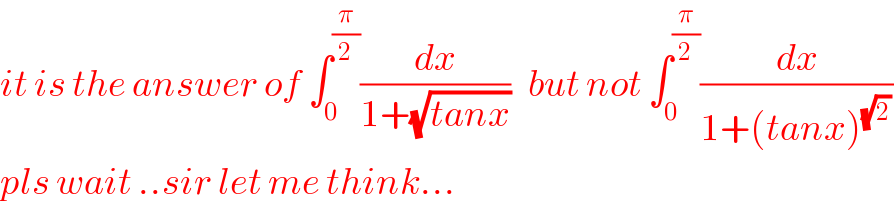
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18

$$4){\int }_0^1\frac{x^a-1}{lnx}dx$$$$I\left(a\right)={\int }_0^1\frac{x^a-1}{lnx}dx$$$$\frac{dI\left(a\right)}{da}={\int }_0^1\frac{\partial }{\partial a}\left(\frac{x^a-1}{lnx}\right)dx$$$$={\int }_0^1\frac{x^{a}lnx}{lnx}dx$$$$=\mid \frac{x^{a+1}}{a+1}{\mid }_0^1=\frac{1}{a+1}$$$$\int dI\left(a\right)=\int \frac{da}{a+1}$$$$I\left(a\right)=ln(a+1)+c$$$$whena=0I\left(a\right)=0[\int \frac{x^0-1}{lnx}dx=0]$$$$c=0$$$$I\left(a\right)=ln(a+1)$$$$henceI=ln2whena=1$$

Answered by mr W last updated on 26/Dec/18

$$\left(3\right)$$$$\int \frac{{\sin }^{2}x}{x^2}dx$$$$=-\int {\sin }^{2}xd\left(\frac{1}{x}\right)$$$$=-\frac{{\sin }^{2}x}{x}+\int \frac{2\sin x\cos x}{x}dx$$$$=-\frac{{\sin }^{2}x}{x}+\int \frac{\sin 2x}{x}dx$$$$=-\frac{{\sin }^{2}x}{x}+\int \frac{\sin 2x}{2x}d\left(2x\right)$$$${\int }_0^{\mathrm{\infty }}\frac{{\sin }^{2}x}{x^2}dx$$$$=-{\left[\frac{{\sin }^{2}x}{x}\right]}_0^{\mathrm{\infty }}+{\int }_0^{\mathrm{\infty }}\frac{\sin 2x}{2x}d\left(2x\right)$$$$=0+{\int }_0^{\mathrm{\infty }}\frac{\sin t}{t}dt$$$$=\frac{\pi }{2}$$

Commented by behi83417@gmail.com last updated on 26/Dec/18

$$let:f\left(a\right)=\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\frac{{sin}^{2}ax}{x^2}dx$$$$\Rightarrow \frac{df\left(a\right)}{da}=\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\frac{2xsinaxcosax}{x^2}dx=$$$$=\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\frac{sin2ax}{x}dx=2a\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\frac{sint}{t}dt=2a\frac{\pi }{2}=a\pi$$$$\Rightarrow f^{\prime }\left(a\right)=a\pi \Rightarrow f\left(a\right)=\pi \frac{a^2}{2}+C.$$$$f\left(0\right)=0\Rightarrow C=0\Rightarrow f\left(a\right)=\frac{\pi .a^2}{2}$$$$if:a=1then:f\left(1\right)=\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\frac{{sin}^{2}x}{x^2}dx=\frac{\pi }{2}.$$

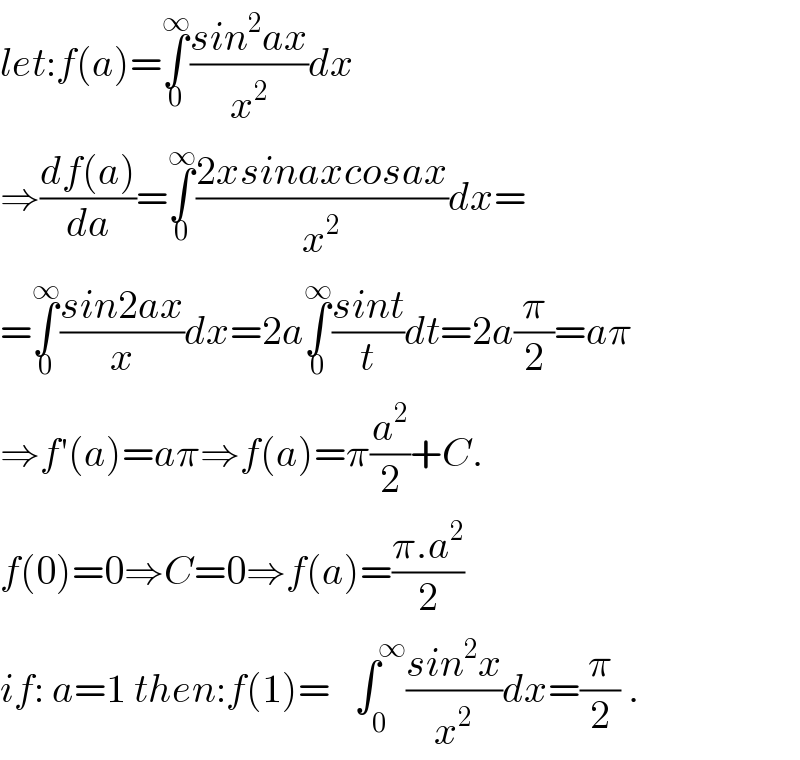
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18

$$1){\int }_0^{\frac{\pi }{2}}\frac{dx}{1+{\left(tanx\right)}^a}[[a=\sqrt{2}]$$$${\int }_0^{\frac{\pi }{2}}\frac{dx}{1+\frac{{\left(sinx\right)}^a}{{\left(cosx\right)}^a}}$$$$I={\int }_0^{\frac{\pi }{2}}\frac{{\left(cosx\right)}^a}{{\left(sinx\right)}^a+{\left(cosx\right)}^a}dx$$$$nowusing{\int }_0^{\frac{\pi }{2}}f\left(x\right)dx={\int }_0^{\frac{\pi }{2}}f(\frac{\pi }{2}-x)dx$$$$2I={\int }_0^{\frac{\pi }{2}}dxI=\frac{\pi }{4}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com