Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 52356 by Tawa1 last updated on 06/Jan/19

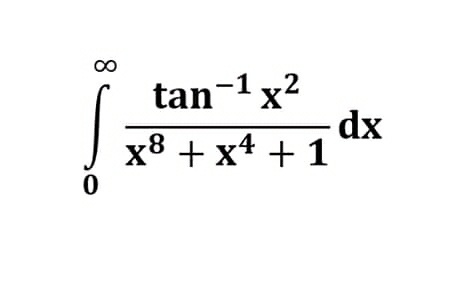
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Jan/19

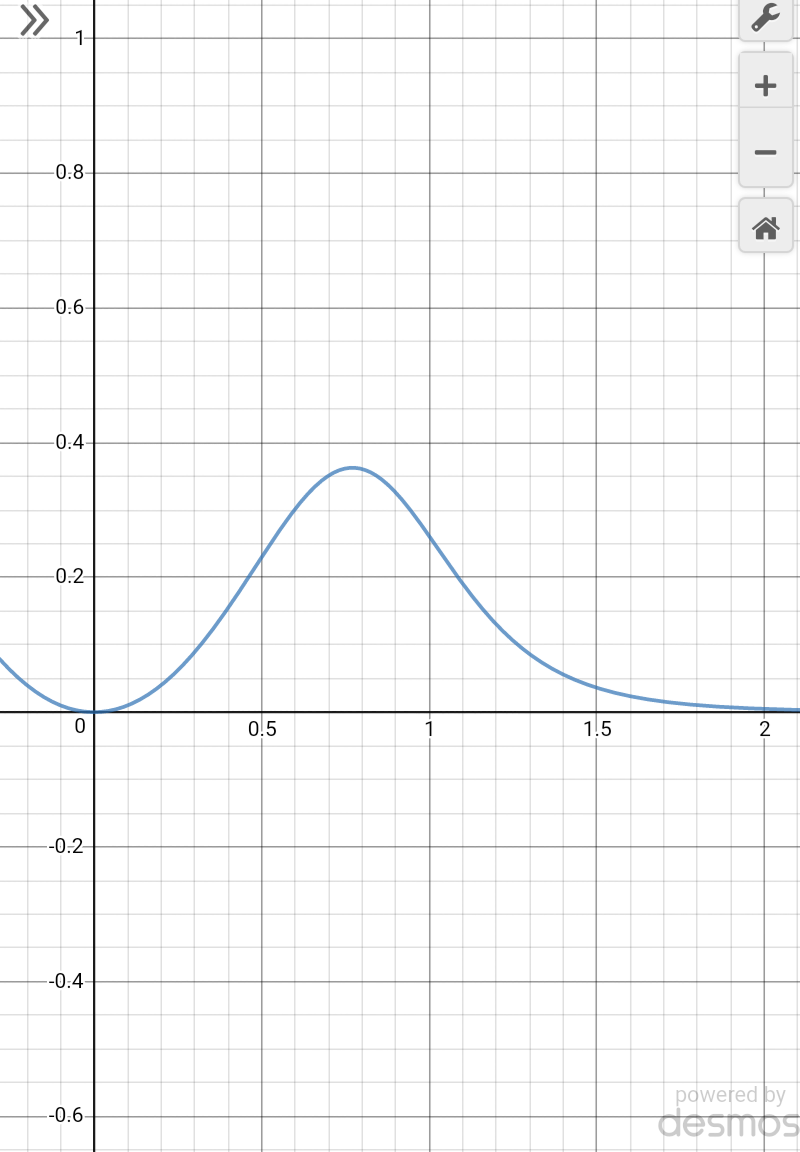
Commented by Tawa1 last updated on 07/Jan/19

$Sir please help .$
Commented by MJS last updated on 07/Jan/19

$this {can}^{'} t be solved using elementary calculus$ $not sure if these help :$ $\tan^{- 1} θ = \frac{i}{2} (\ln (1 - i θ) - \ln (1 + i θ)) \Rightarrow$ $\Rightarrow \tan^{- 1} x^{2} = \frac{i}{2} (\ln (1 - i x^{2}) - \ln (1 + i x^{2})) \Rightarrow$ $\Rightarrow \tan^{- 1} x^{2} = \frac{i}{2} \ln \frac{1 - i x^{2}}{1 + i x^{2}} = \frac{i}{2} \ln \frac{1 - x^{4} + 2 i x^{2}}{x^{4} + 1} =$ $[\ln (a + b i) = \frac{1}{2} \ln (a^{2} + b^{2}) + i (sign (b) \frac{π}{2} - \tan^{- 1} \frac{a}{b})]$ $= \frac{π}{4} + \frac{1}{2} \tan^{- 1} \frac{x^{4} - 1}{2 x^{2}}$ $x^{8} + x^{4} + 1 = (x^{4} + x^{2} + 1) (x^{4} - x^{2} + 1) =$ $= (x^{2} + x + 1) (x^{2} - x + 1) (x^{2} + \sqrt{3} x + 1) (x^{2} - \sqrt{3} x + 1$ $= (x + \frac{1 + i \sqrt{3}}{2}) (x - \frac{1 + i \sqrt{3}}{2}) (x + \frac{1 - i \sqrt{3}}{2}) (x - \frac{1 - i \sqrt{3}}{2}) (x + \frac{\sqrt{3} + i}{2}) (x - \frac{\sqrt{3} + i}{2}) (x + \frac{\sqrt{3} - i}{2}) (x - \frac{\sqrt{3} - i}{2})$
Commented by Tawa1 last updated on 07/Jan/19

$God bless you sir$
Commented by Abdo msup. last updated on 07/Jan/19

$l e t I = \int_{0}^{\infty} \frac{a r c t a n (x^{2})}{x^{8} + x^{4} + 1} d x c h a n g e m e n t x^{2} = t a n t$ $g i v e I = \int_{0}^{\frac{π}{2}} \frac{t}{{t a n}^{4} t + {t a n}^{2} t + 1} \frac{1 + {t a n}^{2} t}{2 \sqrt{1 + {t a n}^{2} t}} d t$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{t \sqrt{1 + {t a n}^{2} t}}{1 + {t a n}^{2} t + {t a n}^{4} t} d t$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{t}{c o s t (\frac{1}{{c o s}^{2} t} + {(1 + {t a n}^{2} t - 1)}^{2})} d t$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{t}{\frac{1}{c o s t} + c o s t {(\frac{1}{{c o s}^{2} t} - 1)}^{2}} d t$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{t}{\frac{1}{c o s t} + c o s s t (\frac{1}{{c o s}^{4} t} - \frac{2}{{c o s}^{2} t} + 1)} d t$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{t}{\frac{1}{c o s t} + \frac{1}{{c o s}^{3} t} - \frac{2}{c o s t} + c o s t} d t$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{t {c o s}^{3} t}{{c o s}^{2} t + 1 - 2 {c o s}^{2} t + {c o s}^{4} t} d t$ $= \frac{1}{2} \int_{0}^{\frac{π}{2}} \frac{t {c o s}^{3} t}{{c o s}^{4} t - {c o s}^{2} t + 1} d t . . . b e c o n t i n u e d . . .$
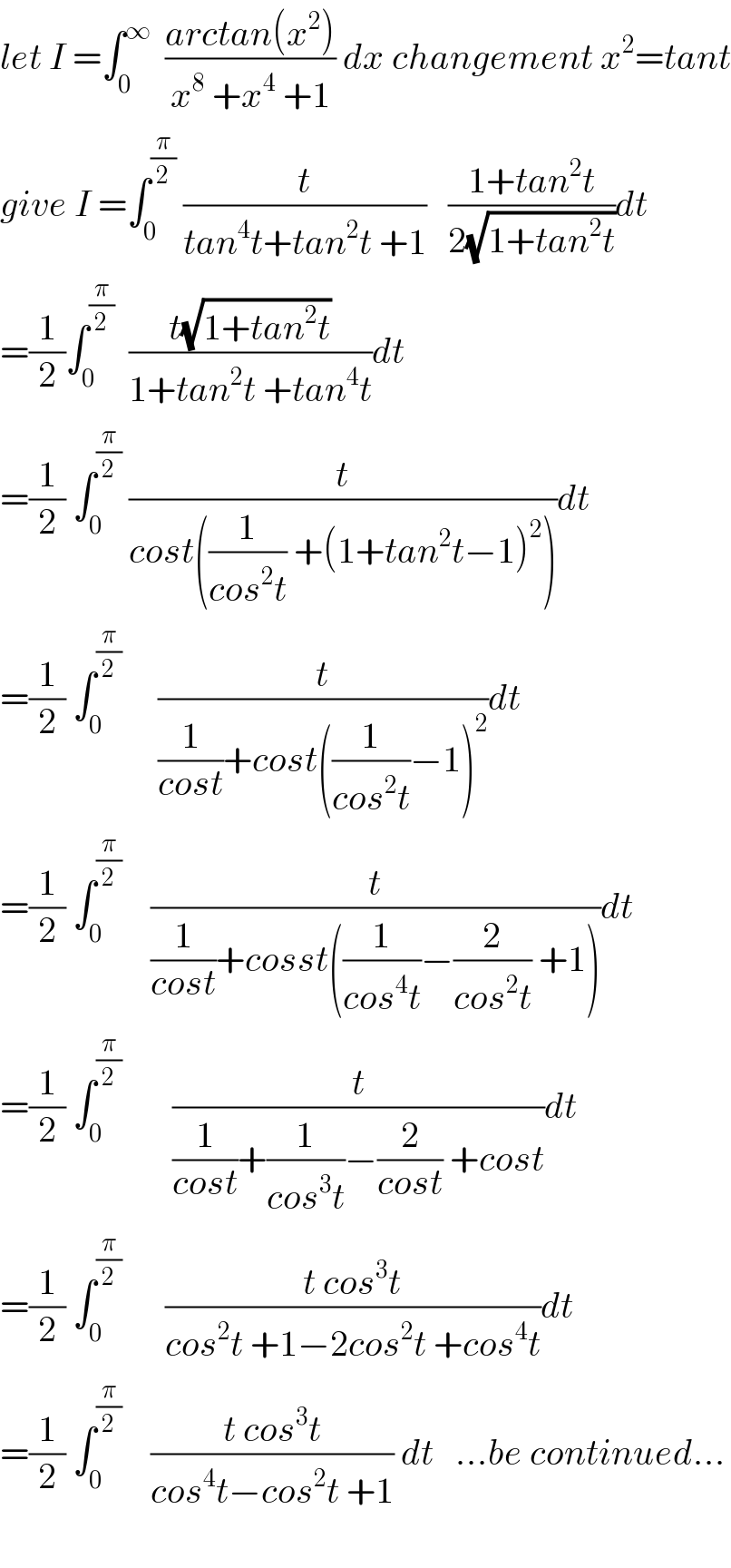
Commented by Abdo msup. last updated on 07/Jan/19
$let F(α)=∫_0 ^∞ ((arctan(αx^2 ))/(1+x^4 +x^8 )) dx with α>0 we have F^′ (α) =∫_0 ^∞ (x^2 /((1+α^2 x^4 )(x^8 +x^4 +1)))dx ⇒2F^′ (α) =∫_(−∞) ^(+∞) (x^2 /((x^8 +x^4 +1)(α^2 x^4 +1)))dx let consider the complex function ϕ(z)=(z^2 /((z^8 +z^4 +1)(α^2 z^4 +1))) poles of ϕ? z^8 +z^4 +1=0 ⇔1+z^4 +(z^4 )^2 =0 ⇔((1−z^(12) )/(1−z^4 )) =0 ⇔ z^(12) =1 and z^4 ≠ 1 the roots of z^(12) =1 are z_k =e^(i((kπ)/6)) and k∈[[0,11]] but only we must take 8 roots let search.. z_0 =1 (to eliminate) z_1 =e^((iπ)/6) and z_1 ^4 ≠1 z_2 =e^((iπ)/3) and z_2 ^4 ≠1 z_3 =e^((iπ)/2) and z_3 ^4 =1 (to eliminate) z_4 =e^(i((2π)/3)) and z_4 ^4 ≠1 z_5 =e^((i5π)/6) and z_5 ^4 ≠1 z_6 =e^(iπ) and z_6 ^4 =1 (to eliminate) z_7 =e^((i7.π)/6) and z_7 ^4 ≠1 z_8 = e^((i4π)/3) and z_8 ^4 ≠1 z_9 = e^((i3π)/2) and z_9 ^4 =1 (to eliminate) z_(10) =e^((i5π)/3) and z_(10) ^4 ≠1 z_(11) =e^((i11π)/6) ⇒ z^8 +z^4 +1 =(z−z_1 )(z−z_2 )(z−z_4 )(z−z_5 )(z−z_7 )(z−z_8 )(z−z_(10) )(z−z_(11) ) also we have α^2 z^4 +1 =α^2 (z^4 +(1/α^2 )) =α^2 (z^4 −((i/α))^2 )=α^2 (z^2 −(i/α))(z^2 +(i/α)) =α^2 (z−(1/(√α)) e^((iπ)/4) )(z+(1/(√α)) e^((iπ)/4) )(z−(1/(√α)) e^(−((iπ)/4)) )(z+(1/(√α))e^(−((iπ)/4)) ) so the poles of ϕ are +^− (1/(√α)) e^((iπ)/4) and +^− (1/(√α)) e^(−((iπ)/4)) also tbe complex z_k with k ∈{1,2,4,5,7,8,10,11} after we use Residus theorem ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Σ_(im(z_k )>0) Res(ϕ ,z_k ) ...be continued ...$
$l e t F (α) = \int_{0}^{\infty} \frac{a r c t a n (α x^{2})}{1 + x^{4} + x^{8}} d x w i t h α > 0 w e$ $h a v e F^{^{'}} (α) = \int_{0}^{\infty} \frac{x^{2}}{(1 + α^{2} x^{4}) (x^{8} + x^{4} + 1)} d x$ $\Rightarrow 2 F^{^{'}} (α) = \int_{- \infty}^{+ \infty} \frac{x^{2}}{(x^{8} + x^{4} + 1) (α^{2} x^{4} + 1)} d x$ $l e t c o n s i d e r t h e c o m p l e x f u n c t i o n$ $φ (z) = \frac{z^{2}}{(z^{8} + z^{4} + 1) (α^{2} z^{4} + 1)} p o l e s o f φ ?$ $z^{8} + z^{4} + 1 = 0 \Leftrightarrow 1 + z^{4} + {(z^{4})}^{2} = 0 \Leftrightarrow \frac{1 - z^{12}}{1 - z^{4}} = 0 \Leftrightarrow$ $z^{12} = 1 a n d z^{4} \neq 1 t h e r o o t s o f z^{12} = 1 a r e$ $z_{k} = e^{i \frac{k π}{6}} a n d k \in [[0, 11]] b u t o n l y w e m u s t t a k e$ $8 r o o t s l e t s e a r c h . .$ $z_{0} = 1 (t o e l i m i n a t e)$ $z_{1} = e^{\frac{i π}{6}} a n d z_{1}^{4} \neq 1$ $z_{2} = e^{\frac{i π}{3}} a n d z_{2}^{4} \neq 1$ $z_{3} = e^{\frac{i π}{2}} a n d z_{3}^{4} = 1 (t o e l i m i n a t e)$ $z_{4} = e^{i \frac{2 π}{3}} a n d z_{4}^{4} \neq 1$ $z_{5} = e^{\frac{i 5 π}{6}} a n d z_{5}^{4} \neq 1$ $z_{6} = e^{i π} a n d z_{6}^{4} = 1 (t o e l i m i n a t e)$ $z_{7} = e^{\frac{i 7 . π}{6}} a n d z_{7}^{4} \neq 1$ $z_{8} = e^{\frac{i 4 π}{3}} a n d z_{8}^{4} \neq 1$ $z_{9} = e^{\frac{i 3 π}{2}} a n d z_{9}^{4} = 1 (t o e l i m i n a t e)$ $z_{10} = e^{\frac{i 5 π}{3}} a n d z_{10}^{4} \neq 1$ $z_{11} = e^{\frac{i 11 π}{6}} \Rightarrow$ $z^{8} + z^{4} + 1 = (z - z_{1}) (z - z_{2}) (z - z_{4}) (z - z_{5}) (z - z_{7}) (z - z_{8}) (z - z_{10}) (z - z_{11})$ $a l s o w e h a v e α^{2} z^{4} + 1 = α^{2} (z^{4} + \frac{1}{α^{2}})$ $= α^{2} (z^{4} - {(\frac{i}{α})}^{2}) = α^{2} (z^{2} - \frac{i}{α}) (z^{2} + \frac{i}{α})$ $= α^{2} (z - \frac{1}{\sqrt{α}} e^{\frac{i π}{4}}) (z + \frac{1}{\sqrt{α}} e^{\frac{i π}{4}}) (z - \frac{1}{\sqrt{α}} e^{- \frac{i π}{4}}) (z + \frac{1}{\sqrt{α}} e^{- \frac{i π}{4}})$ $s o t h e p o l e s o f φ a r e$ $\bar{+} \frac{1}{\sqrt{α}} e^{\frac{i π}{4}} a n d \bar{+} \frac{1}{\sqrt{α}} e^{- \frac{i π}{4}} a l s o t b e c o m p l e x$ $z_{k} w i t h k \in {1, 2, 4, 5, 7, 8, 10, 11} a f t e r w e u s e$ $R e s i d u s t h e o r e m$ $\int_{- \infty}^{+ \infty} φ (z) d z = 2 i π \sum_{i m (z_{k}) > 0} R e s (φ, z_{k})$ $. . . b e c o n t i n u e d . . .$
Commented by Tawa1 last updated on 07/Jan/19

$God bless you sir . waiting . . .$
Commented by Abdo msup. last updated on 07/Jan/19

$t h a n k s s i r t h i s i s t h e w a y f o r t h i s i n t e g r a l . . . .$
	Answered by MJS last updated on 07/Jan/19

	$\approx . 269949$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum