Math Question and Answers


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 53376 by rajeshghorai130@gmail.com last updated on 21/Jan/19

Commented by Abdo msup. last updated on 21/Jan/19

$l e t A (x) = \frac{{(s i n α)}^{x} - {(c o s α)}^{x} - c o s (2 α)}{x - 4}$ $A (x) =_{x - 4 = t} \frac{{(s i n α)}^{t + 4} - {(c o s α)}^{t + 4} - c o s (2 α)}{t} = B (t)$ $\Rightarrow {l i m}_{x \to 4} A (x) = {l i m}_{t \to 0} B (t)$ $B (t) = \frac{{s i n}^{4} α e^{t l n (s i n α)} - {(c o s α)}^{4} e^{t l n (c o s α)} - c o s (2 α)}{t}$ $b u t e^{t l n (s i n α)} \sim 1 + t l n (s i n α) (t \to 0)$ $e^{t l n (c o s α)} \sim 1 + t l n (c o s α) \Rightarrow$ $B (t) \sim \frac{{s i n}^{4} α (1 + t l n (s i n α)) - ({c o s}^{4} α) (1 + t l n (c o s α)) - c o s (2 α)}{t}$ $B (t) \sim \frac{{s i n}^{4} α - {c o s}^{4} α - c o s (2 α) + {t s i n}^{4} α l n (s i n α) - {t c o s}^{4} α l n (c o s α)}{t}$ $\Rightarrow B (t) \sim {s i n}^{4} α l n (s i n α) - {c o s}^{4} α l n (c o s α) (t \to 0)$ $\Rightarrow {l i m}_{x \to 4} A (x) = {l i m}_{t \to 0} B (t)$ ${(s i n α)}^{4} l n (s i n α) - {(c o s α)}^{4} l n (c o s α) .$
	Answered by pooja24 last updated on 21/Jan/19

	$u s i n g l^{'} h o p i t a l r u l e a n s i s 4 ({s i n}^{3} α - {c o s}^{3} α)$
	Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19

	$i t h i n k q u e s t i o n s h o u l d b e$ $\lim_{x \to 4} \frac{{(s i n α)}^{x} - {(c o s α)}^{x} + c o s 2 α}{x - 4} (\frac{0}{0}) f o r m$ $u s i n g L H r u l e$ $\lim_{x \to 4} \frac{{(s i n α)}^{x} l n s i n α - {(c o s α)}^{x} l n c o s α}{1}$ $= {(s i n α)}^{4} l n s i n α - {(c o s α)}^{4} l n c o s α$
	Commented by rajeshghorai130@gmail.com last updated on 21/Jan/19

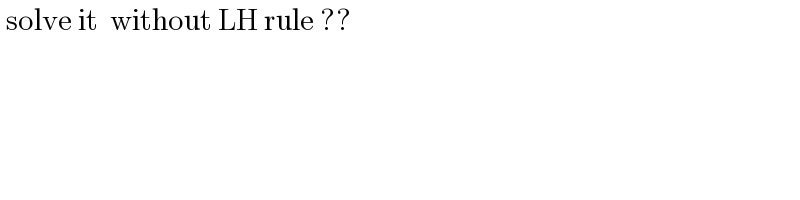
	$solve it without LH rule ? ?$
	Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19

	$i s i t a r e q u e s t . . . l a n g u a g e . . s e e m o t h e r w i s e$
	Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19

	$w i t h o u t L H r u l e . . .$ $t = x - 4$ $\lim_{t \to 0} \frac{{(s i n α)}^{t + 4} - {(c o s α)}^{t + 4} + {c o s}^{2} α - {s i n}^{2} α}{t}$ $\lim_{t \to 0} \frac{{({s i n}^{} α)}^{t + 4} - {(c o s α)}^{t + 4} + ({c o s}^{2} α - {s i n}^{2} α) ({c o s}^{2} α + {s i n}^{2} α) \leftarrow t r i c k s}{t}$ $= \lim_{t \to 0} [\frac{{s i n}^{4} α ({s i n}^{t} α - 1)}{t} - \frac{{c o s}^{4} α ({c o s}^{t} α - 1)}{t}]$ $= {s i n}^{4} α \times l n s i n α - {c o s}^{4} α \times l n c o s α (p r o v e d)$ $u s e d f o r m u l a$ $\lim_{x \to 0} \frac{a^{x} - 1}{x} = l n a$ $N$ $\underset{x \to 0}{li}$ $\lim_{x \to 0} \frac{a^{x} - 1}{x}$ $= \underset{x \to 0}{li}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum