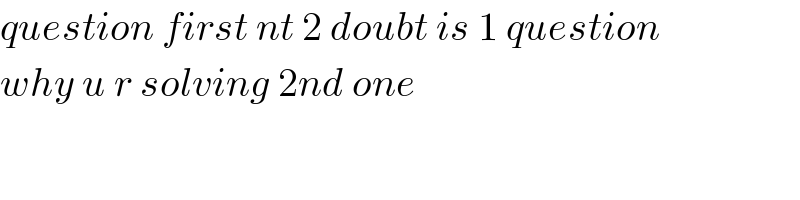Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 60367 by bhanukumarb2@gmail.com last updated on 20/May/19

Commented by bhanukumarb2@gmail.com last updated on 20/May/19

$$1$$

Commented by Mr X pcx last updated on 20/May/19

$$I_2={\int }_0^1\frac{dx}{{(1+x^2)}^2}vhangementx=tan\theta$$$$give{I}_2={\int }_0^{\frac{\pi }{4}}\frac{1+{tan}^2\theta }{{(1+{tan}^2\theta )}^2}d\theta$$$$={\int }_0^{\frac{\pi }{4}}\frac{d\theta }{1+{tan}^2\theta }={\int }_0^{\frac{\pi }{4}}{cos}^2\theta d\theta$$$$={\int }_0^{\frac{\pi }{4}}\frac{1+cos\left(2\theta \right)}{2}d\theta =\frac{\pi }{8}+{\left[\frac{1}{4}sin\left(2\theta \right)\right]}_0^{\frac{\pi }{4}}$$$$=\frac{\pi }{8}+\frac{1}{4}sotheanswer\left(B\right)iscorrect.$$

Commented by bhanukumarb2@gmail.com last updated on 20/May/19

$$1questionsir$$

Commented by Mr X pcx last updated on 20/May/19

$$wehave{I}_n={\int }_0^1\frac{dx}{{(1+x^2)}^n}$$$$={\int }_0^1\frac{1+x^2}{{(1+x^2)}^{n+1}}dx=I_{n+1}+{\int }_0^{1}x\frac{x}{{(1+x^2)}^{n+1}}dx$$$$bypartsu=xand{v}^{{}^{\prime }}=x{(1+x^2)}^{-n-1}$$$${\int }_0^{1}x\frac{x}{{(1+x^2)}^{n+1}}dx=[x{(-\frac{1}{2n}{(1+x^2)}^{-n}]}_0^1$$$$-{\int }_0^{1}1.(-\frac{1}{2n}{(1+x^2)}^{-n})dx$$$$=-\frac{1}{2n}{2}^{-n}+\frac{1}{2n}{I}_n\Rightarrow I_n=I_{n+1}+\frac{1}{2n}{I}_n$$$$-\frac{1}{2n}{2}^{-n}\Rightarrow (1-\frac{1}{2n})I_n=I_{n+1}-\frac{1}{2n}{2}^{-n}$$$$\Rightarrow (2n-1)I_n=2n{I}_{n+1}-\frac{1}{2^n}\Rightarrow$$$$2n{I}_{n+1}=\frac{1}{2^n}+(2n-1)I_n$$

Commented by Mr X pcx last updated on 20/May/19

$$option\left(A\right)istrue.$$

Commented by bhanukumarb2@gmail.com last updated on 21/May/19

$$questionfirstnt2doubtis1question$$$$whyursolving2ndone$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com