Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 61762 by mr W last updated on 08/Jun/19

Commented by mr W last updated on 08/Jun/19

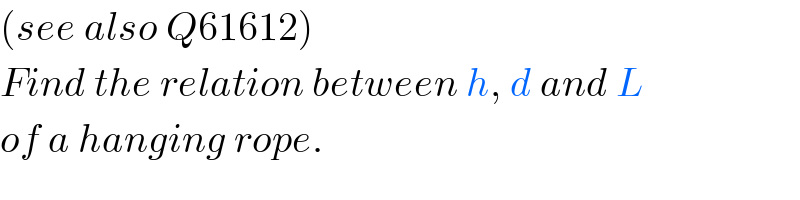
$(s e e a l s o Q 61612)$ $F i n d t h e r e l a t i o n b e t w e e n h, d a n d L$ $o f a h a n g i n g r o p e .$
	Answered by mr W last updated on 09/Jun/19
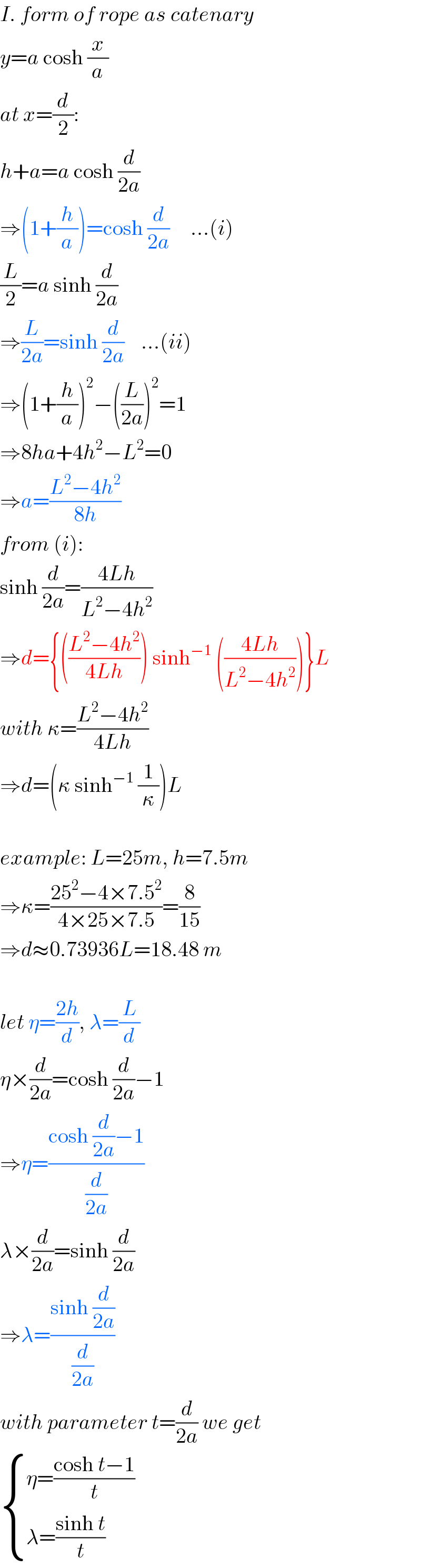
	$I. form of rope as catenary y=a cosh (x/a) at x=(d/2): h+a=a cosh (d/(2a)) ⇒(1+(h/a))=cosh (d/(2a)) ...(i) (L/2)=a sinh (d/(2a)) ⇒(L/(2a))=sinh (d/(2a)) ...(ii) ⇒(1+(h/a))^2 −((L/(2a)))^2 =1 ⇒8ha+4h^2 −L^2 =0 ⇒a=((L^2 −4h^2 )/(8h)) from (i): sinh (d/(2a))=((4Lh)/(L^2 −4h^2 )) ⇒d={(((L^2 −4h^2 )/(4Lh))) sinh^(−1) (((4Lh)/(L^2 −4h^2 )))}L with κ=((L^2 −4h^2 )/(4Lh)) ⇒d=(κ sinh^(−1) (1/κ))L example: L=25m, h=7.5m ⇒κ=((25^2 −4×7.5^2 )/(4×25×7.5))=(8/(15)) ⇒d≈0.73936L=18.48 m let η=((2h)/d), λ=(L/d) η×(d/(2a))=cosh (d/(2a))−1 ⇒η=((cosh (d/(2a))−1)/(d/(2a))) λ×(d/(2a))=sinh (d/(2a)) ⇒λ=((sinh (d/(2a)))/(d/(2a))) with parameter t=(d/(2a)) we get { ((η=((cosh t−1)/t))),((λ=((sinh t)/t))) :}$
	$I . f o r m o f r o p e a s c a t e n a r y$ $y = a \cosh \frac{x}{a}$ $a t x = \frac{d}{2} :$ $h + a = a \cosh \frac{d}{2 a}$ $\Rightarrow (1 + \frac{h}{a}) = \cosh \frac{d}{2 a} . . . (i)$ $\frac{L}{2} = a \sinh \frac{d}{2 a}$ $\Rightarrow \frac{L}{2 a} = \sinh \frac{d}{2 a} . . . (i i)$ $\Rightarrow {(1 + \frac{h}{a})}^{2} - {(\frac{L}{2 a})}^{2} = 1$ $\Rightarrow 8 h a + 4 h^{2} - L^{2} = 0$ $\Rightarrow a = \frac{L^{2} - 4 h^{2}}{8 h}$ $f r o m (i) :$ $\sinh \frac{d}{2 a} = \frac{4 L h}{L^{2} - 4 h^{2}}$ $\Rightarrow d = {(\frac{L^{2} - 4 h^{2}}{4 L h}) \sinh^{- 1} (\frac{4 L h}{L^{2} - 4 h^{2}})} L$ $w i t h κ = \frac{L^{2} - 4 h^{2}}{4 L h}$ $\Rightarrow d = (κ \sinh^{- 1} \frac{1}{κ}) L$ $e x a m p l e : L = 25 m, h = 7.5 m$ $\Rightarrow κ = \frac{25^{2} - 4 \times 7 . 5^{2}}{4 \times 25 \times 7.5} = \frac{8}{15}$ $\Rightarrow d \approx 0.73936 L = 18.48 m$ $l e t η = \frac{2 h}{d}, λ = \frac{L}{d}$ $η \times \frac{d}{2 a} = \cosh \frac{d}{2 a} - 1$ $\Rightarrow η = \frac{\cosh \frac{d}{2 a} - 1}{\frac{d}{2 a}}$ $λ \times \frac{d}{2 a} = \sinh \frac{d}{2 a}$ $\Rightarrow λ = \frac{\sinh \frac{d}{2 a}}{\frac{d}{2 a}}$ $w i t h p a r a m e t e r t = \frac{d}{2 a} w e g e t$ ${\begin{cases} η = \frac{\cosh t - 1}{t} \\ λ = \frac{\sinh t}{t} \end{cases}$
	Commented by Tawa1 last updated on 09/Jun/19

	$wow, God bless you sir$
	Answered by mr W last updated on 08/Jun/19

	$I I . f o r m o f r o p e a s p a r a b o l a$ $y = h {(\frac{2 x}{d})}^{2}$ $y^{'} = \frac{8 h x}{d^{2}}$ $\frac{L}{2} = \int_{0}^{\frac{d}{2}} \sqrt{1 + y^{' 2}} d x = \int_{0}^{\frac{d}{2}} \sqrt{1 + {(\frac{8 h x}{d^{2}})}^{2}} d x$ $L = \frac{d^{2}}{4 h} \int_{0}^{\frac{d}{2}} \sqrt{1 + {(\frac{8 h x}{d^{2}})}^{2}} d (\frac{8 h x}{d^{2}})$ $L = \frac{d^{2}}{4 h} \int_{0}^{\frac{4 h}{d}} \sqrt{1 + t^{2}} d t$ $L = 2 h {(\frac{d}{4 h})}^{2} {[t \sqrt{1 + t^{2}} + \ln (t + \sqrt{1 + t^{2}})]}_{0}^{\frac{4 h}{d}}$ $w i t h μ = \frac{4 h}{d}$ $\Rightarrow L = \frac{2 h}{μ^{2}} [μ \sqrt{1 + μ^{2}} + \ln (μ + \sqrt{1 + μ^{2}})]$ $\Rightarrow \frac{L}{2 h} = \frac{1}{μ^{2}} [μ \sqrt{1 + μ^{2}} + \ln (μ + \sqrt{1 + μ^{2}})]$ $e x a m p l e : L = 25 m, h = 7.5 m$ $\frac{1}{μ^{2}} [μ \sqrt{1 + μ^{2}} + \ln (μ + \sqrt{1 + μ^{2}})] = \frac{5}{3}$ $\Rightarrow μ = 1.6008$ $\Rightarrow d = \frac{4 h}{μ} = 18.74 m$ $l e t η = \frac{2 h}{d}, λ = \frac{L}{d}$ $\Rightarrow λ = \frac{1}{4 η} [2 η \sqrt{1 + 4 η^{2}} + \ln (2 η + \sqrt{1 + 4 η^{2}})]$
	Commented by mr W last updated on 08/Jun/19

	Commented by mr W last updated on 08/Jun/19

	$C = c a t e n a r y, P = p a r a b o l a$ $w e c a n s e e t h e d i f f e r e n c e b e t w e e n b o t h$ $i s v e r y s m a l l .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum