
Question and Answers Forum
Question Number 61809 by aliesam last updated on 09/Jun/19

Commented by maxmathsup by imad last updated on 10/Jun/19
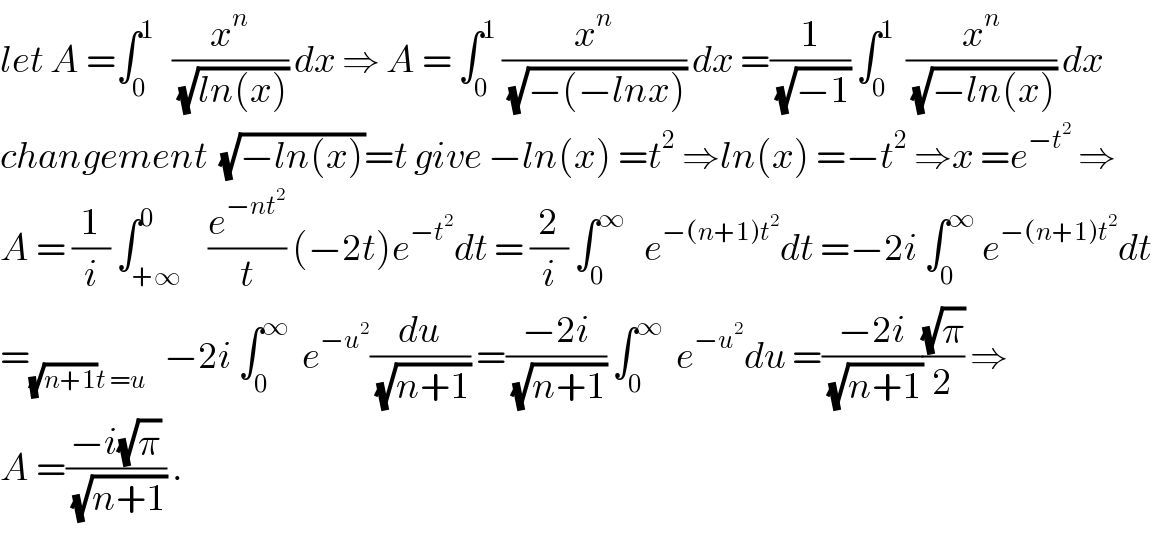
Answered by perlman last updated on 09/Jun/19
![(√(ln(x)))=i(√(−ln(x))) ∀x∈]0;1] withe (√(−ln(x)))=y x=e^(−y^2 ) =∫_(+∞) ^0 (e^(−ny^2 ) /(iy))(−2y)e^(−y^2 ) dy =i∫_0 ^(+∞) e^(−(n+1)y^2 ) dy let z=(√((n+1)))y dz=(√(n+1))dy =i∫_0 ^(+∞) (√(n+1))e^(−z^2 ) dz=i(√(n+1))∫_0 ^(+∞) e^(−z^2 ) dz=i(√(n+1))((√π)/2)](Q61813.png)
| ||
Question and Answers Forum | ||
Question Number 61809 by aliesam last updated on 09/Jun/19 | ||
 | ||
Commented by maxmathsup by imad last updated on 10/Jun/19 | ||
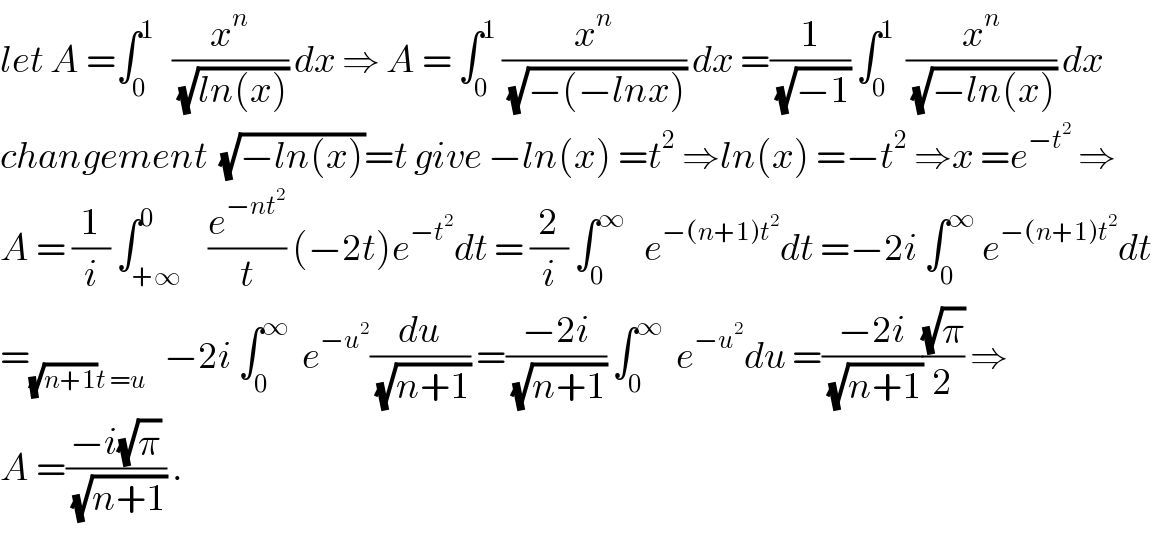 | ||
Answered by perlman last updated on 09/Jun/19 | ||
![(√(ln(x)))=i(√(−ln(x))) ∀x∈]0;1] withe (√(−ln(x)))=y x=e^(−y^2 ) =∫_(+∞) ^0 (e^(−ny^2 ) /(iy))(−2y)e^(−y^2 ) dy =i∫_0 ^(+∞) e^(−(n+1)y^2 ) dy let z=(√((n+1)))y dz=(√(n+1))dy =i∫_0 ^(+∞) (√(n+1))e^(−z^2 ) dz=i(√(n+1))∫_0 ^(+∞) e^(−z^2 ) dz=i(√(n+1))((√π)/2)](Q61813.png) | ||
| ||