
Question and Answers Forum
Question Number 61834 by aliesam last updated on 09/Jun/19

Commented by maxmathsup by imad last updated on 09/Jun/19
![let A_n = {(1/p) Σ_(k=1) ^p (1+(k/p))^(1/n) }^n ⇒ln(A_n ) =n ln((1/p)Σ_(k=1) ^p (1+(k/p))^(1/n) ) we have lim_(p→+∞) (1/p)Σ_(k=1) ^p (1+(k/p))^(1/n) =∫_0 ^1 (1+x)^(1/n) dx =[(1/(1+(1/n)))(1+x)^((1/n)+1) ]_0 ^1 =(n/(n+1)) {2^((n+1)/n) −1} ⇒ln(A_n ) = n ln{(n/(n+1))( 2^(1+(1/n)) −1)} we have 2^(1+(1/n)) −1 =2 e^((ln(2))/n) −1 ∼2{ 1 +((ln(2))/n)} −1 =1+(2/n)ln(2)⇒ (n/(n+1))(2^(1+(1/n)) −1) ∼(n/(n+1))(1+(2/n)ln(2)) =(n/(n+1)) +(2/(n+1))ln(2) ⇒ nln{(n/(n+1))(2^(1+(1/n)) −1)} ∼ nln((n/(n+1)) +(2/(n+1))ln(2)) but nln((n/(n+1)) +((2ln(2))/(n+1))) =n ln(1−(1/(n+1)) +((2ln(2))/(n+1))) ∼n(−(1/(n+1)) +((2ln(2))/(n+1))) =(n/(n+1)){−1+2ln(2)}→2ln(2)−1 ⇒ lim_(n→+∞) A_n =e^(2ln(2)−1) =(4/e) ⇒ lim_(n→+∞) X_n =(4/e) .](Q61836.png)
Commented by aliesam last updated on 09/Jun/19
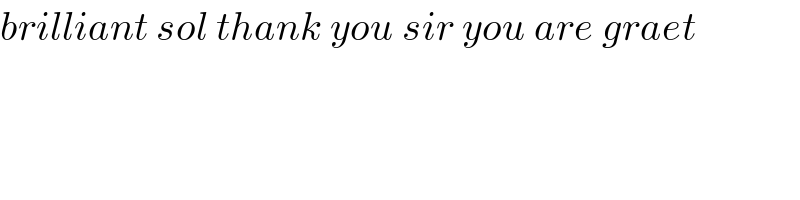
Commented by maxmathsup by imad last updated on 09/Jun/19

| ||
Question and Answers Forum | ||
Question Number 61834 by aliesam last updated on 09/Jun/19 | ||
 | ||
Commented by maxmathsup by imad last updated on 09/Jun/19 | ||
![let A_n = {(1/p) Σ_(k=1) ^p (1+(k/p))^(1/n) }^n ⇒ln(A_n ) =n ln((1/p)Σ_(k=1) ^p (1+(k/p))^(1/n) ) we have lim_(p→+∞) (1/p)Σ_(k=1) ^p (1+(k/p))^(1/n) =∫_0 ^1 (1+x)^(1/n) dx =[(1/(1+(1/n)))(1+x)^((1/n)+1) ]_0 ^1 =(n/(n+1)) {2^((n+1)/n) −1} ⇒ln(A_n ) = n ln{(n/(n+1))( 2^(1+(1/n)) −1)} we have 2^(1+(1/n)) −1 =2 e^((ln(2))/n) −1 ∼2{ 1 +((ln(2))/n)} −1 =1+(2/n)ln(2)⇒ (n/(n+1))(2^(1+(1/n)) −1) ∼(n/(n+1))(1+(2/n)ln(2)) =(n/(n+1)) +(2/(n+1))ln(2) ⇒ nln{(n/(n+1))(2^(1+(1/n)) −1)} ∼ nln((n/(n+1)) +(2/(n+1))ln(2)) but nln((n/(n+1)) +((2ln(2))/(n+1))) =n ln(1−(1/(n+1)) +((2ln(2))/(n+1))) ∼n(−(1/(n+1)) +((2ln(2))/(n+1))) =(n/(n+1)){−1+2ln(2)}→2ln(2)−1 ⇒ lim_(n→+∞) A_n =e^(2ln(2)−1) =(4/e) ⇒ lim_(n→+∞) X_n =(4/e) .](Q61836.png) | ||
Commented by aliesam last updated on 09/Jun/19 | ||
 | ||
Commented by maxmathsup by imad last updated on 09/Jun/19 | ||
 | ||