Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 62112 by aliesam last updated on 15/Jun/19

Answered by MJS last updated on 15/Jun/19

$${\sin }^{10}x+{\cos }^{10}x=\frac{11}{36}$$$$\frac{5}{128}\cos 8x+\frac{15}{32}\cos 4x+\frac{63}{128}=\frac{11}{36}$$$$\cos 8x+12\cos 4x+\frac{43}{9}=0$$$$x=\frac{1}{2}\arctan t$$$$-\frac{56t^4-32t^2-160}{9{(t^2+1)}^2}=0$$$$\frac{(t^2-2)(7t^2+10)}{{(t^2+1)}^2}=0$$$$\Rightarrow t=\pm \sqrt{2}$$$$$$$${\sin }^{12}x+{\cos }^{12}x=\frac{1}{1024}\cos 12x+\frac{33}{512}\cos 8x+\frac{495}{1024}\cos 4x+\frac{231}{512}=$$$$=\frac{(t^2+2)(t^4+16t^2+16)}{32{(t^2+1)}^3}=\frac{13}{54}$$$$m+n=67$$

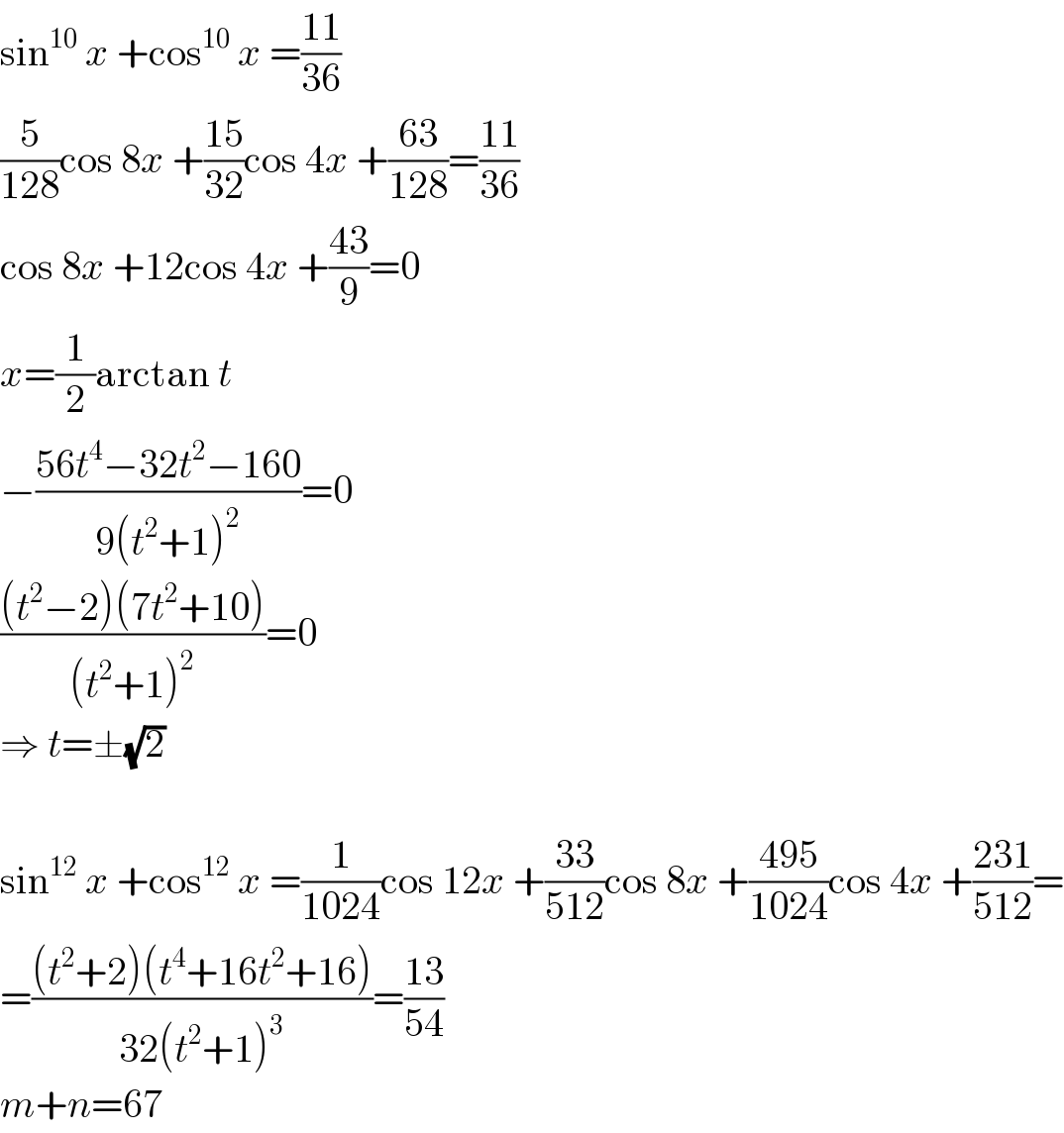
Commented by MJS last updated on 15/Jun/19

$$\mathrm{please}\mathrm{study}\mathrm{the}\mathrm{transformation}\mathrm{formulas}$$$$\mathrm{of}\mathrm{the}\mathrm{trigonometric}\mathrm{functions}.{\mathrm{I}}^{\prime }\mathrm{m}\mathrm{too}\mathrm{busy}$$$$\mathrm{to}\mathrm{type}\mathrm{them}\mathrm{all}$$

Commented by aliesam last updated on 15/Jun/19

$$okiwillandthankyousir$$

Answered by mr W last updated on 15/Jun/19

$${\sin }^{10}x+{\cos }^{10}x=\frac{11}{36}$$$${\left({\sin }^{2}x\right)}^5+{\left({\cos }^{2}x\right)}^5=\frac{11}{36}$$$$({\sin }^{2}x+{\cos }^{2}x)({\sin }^{8}x-{\sin }^{6}x{\cos }^{2}x+{\sin }^{4}x{\cos }^{4}x-{\sin }^{2}x{\cos }^{6}x+{\cos }^{8}x)=\frac{11}{36}$$$${({\sin }^{4}x+{\cos }^{4}x)}^2-{\sin }^{6}x{\cos }^{2}x-{\sin }^{4}x{\cos }^{4}x-{\sin }^{2}x{\cos }^{6}x=\frac{11}{36}$$$${(1-2{\sin }^{2}x{\cos }^{2}x)}^2-{\sin }^{2}x{\cos }^{2}x(1-2{\sin }^{2}x{\cos }^{2}x)-{\sin }^{4}x{\cos }^{4}x=\frac{11}{36}$$$$lets={\sin }^{2}x{\cos }^{2}x=\frac{{\sin }^{2}2x}{4}⩽\frac{1}{4}$$$${(1-2s)}^2-s(1-2s)-s^2=\frac{11}{36}$$$$\Rightarrow s^2-s+\frac{5}{36}=0$$$$\Rightarrow s=\frac{1}{2}(1\pm \frac{2}{3})=\frac{1}{6},\frac{5}{6}\Rightarrow s=\frac{1}{6}<\frac{1}{4}$$$$$$$${\sin }^{12}x+{\cos }^{12}x$$$$={\left({\sin }^{4}x\right)}^3+{\left({\cos }^{4}x\right)}^3$$$$=({\sin }^{4}x+{\cos }^{4}x)({\sin }^{8}x-{\sin }^{4}x{\cos }^{4}x+{\cos }^{8}x)$$$$=(1-2{\sin }^{2}x{\cos }^{2}x)[{({\sin }^{4}x+{\cos }^{4}x)}^2-3{\sin }^{4}x{\cos }^{4}x]$$$$=(1-2{\sin }^{2}x{\cos }^{2}x)[{(1-2{\sin }^{2}x{\cos }^{2}x)}^2-3{\sin }^{4}x{\cos }^{4}x]$$$$=(1-2s)[{(1-2s)}^2-3s^2]$$$$=(1-\frac{1}{3})[{(1-\frac{1}{3})}^2-3\times \frac{1}{6^2}]$$$$=\frac{2}{3}[\frac{4}{9}-\frac{1}{12}]$$$$=\frac{13}{54}=\frac{m}{n}$$$$\Rightarrow m+n=13+54=67$$$$$$$$generally:$$$$if{\sin }^{10}x+{\cos }^{10}x=a(\frac{1}{16}⩽a⩽1)$$$$then$$$${\sin }^{12}x+{\cos }^{12}x=\frac{1}{2}\sqrt{\frac{1+4a}{5}}(\frac{2a-7}{5}+3\sqrt{\frac{1+4a}{5}})$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com