
Question and Answers Forum
Question Number 62981 by hovea cw last updated on 27/Jun/19

Commented by mathmax by abdo last updated on 27/Jun/19
![2) let A =∫_0 ^(2π) ((x∣sin(2x)∣)/(3+sin^2 x)) dx changement x =π +t give A =∫_(−π) ^π (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt = ∫_(−π) ^0 (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt +∫_0 ^π (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt ∫_(−π) ^0 (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt =_(t=−u) −∫_0 ^π (((π−u)∣sin(2u)∣)/(3+sin^2 u))(−du) ⇒ A = ∫_0 ^π (((π+t+π−t)∣sin(2t)∣)/(3+sin^2 t)) dt =2π ∫_0 ^π ((∣sin(2t)∣)/(3+sin^2 t))dt =_(2t =x) 2π ∫_0 ^(2π) ((∣sin(x)∣)/(3+sin^2 ((x/2)))) (dx/2) =π { ∫_0 ^π ((sinx)/(3+sin^2 ((x/2))))dx +∫_π ^(2π) ((∣sinx∣)/(3+sin^2 ((x/2))))dx} ∫_π ^(2π) ((∣sinx∣)/(3+sin^2 ((x/2))))dx =_(x =π +α) ∫_0 ^π ((sin(α))/(3+sin^2 ((π/2)+(α/2)))) dα =∫_0 ^π ((sin(α))/(3+cos^2 ((α/2))))dα ⇒ A =π { ∫_0 ^π ((sin(x))/(3+sin^2 ((x/2))))dx +∫_0 ^π ((sinx)/(3+cos^2 ((x/2))))dx} =π ∫_0 ^π sinx(7/((3+sin^2 ((x/2)))(3+cos^2 ((x/2))))dx =7π ∫_0 ^π ((sinx)/((3+((1−cosx)/2))(3+((1+cosx)/2))))dx =28π∫_0 ^π sinx{(1/(7−cosx)) +(1/(7+cosx))}dx =28π { ∫_0 ^π ((sinx)/(7−cosx))dx +∫_0 ^π ((sinx)/(7 +cosx))dx} =28π{ [ln∣7−cosx∣]_0 ^π −[ln∣7+cosx∣]_0 ^π } =28π{ ln(8)−ln(6)−ln(6) +ln(8)} =28π{2ln(8)−2ln(6)} =56π{ln(8)−ln(6)} =56π{3ln(2)−ln(2)−ln(3)} ⇒ A =56π{2ln(2)−ln(3)} .](Q62992.png)
Answered by Hope last updated on 27/Jun/19
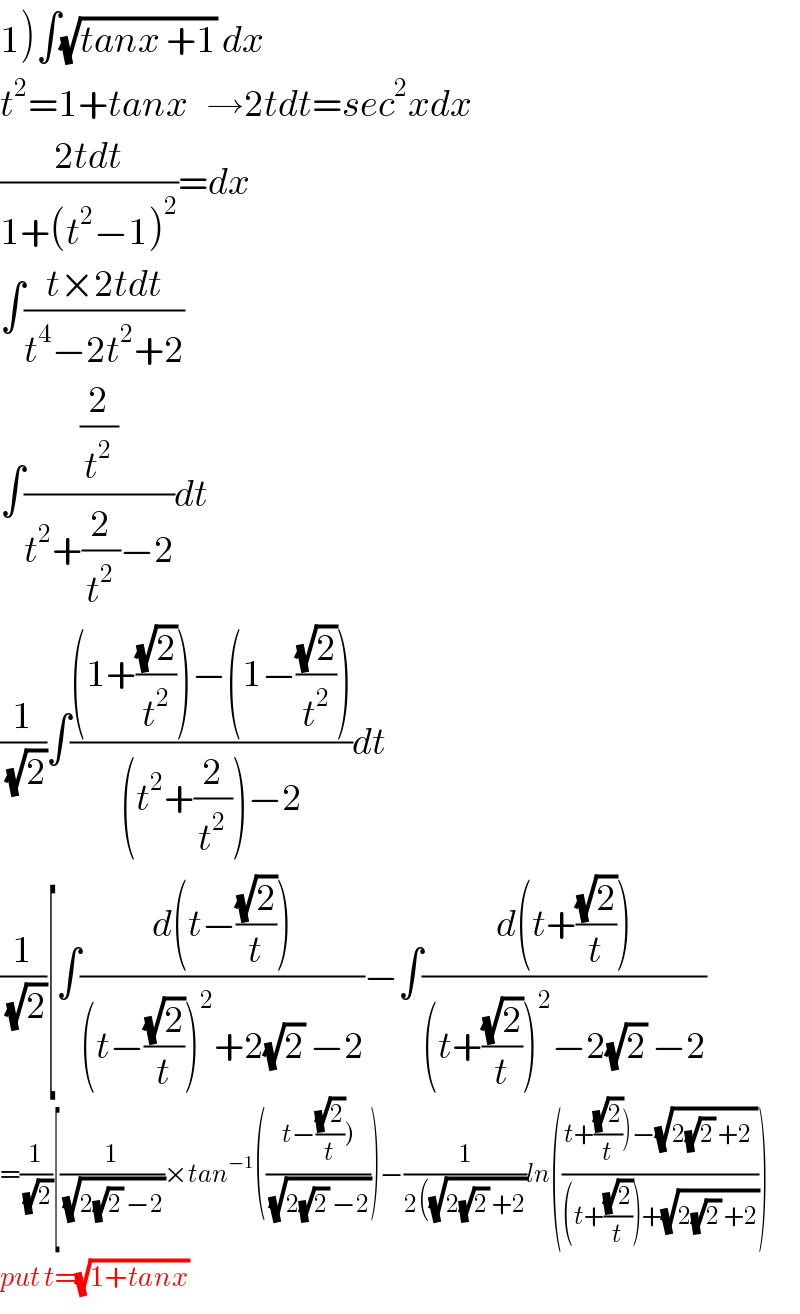
| ||
Question and Answers Forum | ||
Question Number 62981 by hovea cw last updated on 27/Jun/19 | ||
 | ||
Commented by mathmax by abdo last updated on 27/Jun/19 | ||
![2) let A =∫_0 ^(2π) ((x∣sin(2x)∣)/(3+sin^2 x)) dx changement x =π +t give A =∫_(−π) ^π (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt = ∫_(−π) ^0 (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt +∫_0 ^π (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt ∫_(−π) ^0 (((π+t)∣sin(2t)∣)/(3+sin^2 t)) dt =_(t=−u) −∫_0 ^π (((π−u)∣sin(2u)∣)/(3+sin^2 u))(−du) ⇒ A = ∫_0 ^π (((π+t+π−t)∣sin(2t)∣)/(3+sin^2 t)) dt =2π ∫_0 ^π ((∣sin(2t)∣)/(3+sin^2 t))dt =_(2t =x) 2π ∫_0 ^(2π) ((∣sin(x)∣)/(3+sin^2 ((x/2)))) (dx/2) =π { ∫_0 ^π ((sinx)/(3+sin^2 ((x/2))))dx +∫_π ^(2π) ((∣sinx∣)/(3+sin^2 ((x/2))))dx} ∫_π ^(2π) ((∣sinx∣)/(3+sin^2 ((x/2))))dx =_(x =π +α) ∫_0 ^π ((sin(α))/(3+sin^2 ((π/2)+(α/2)))) dα =∫_0 ^π ((sin(α))/(3+cos^2 ((α/2))))dα ⇒ A =π { ∫_0 ^π ((sin(x))/(3+sin^2 ((x/2))))dx +∫_0 ^π ((sinx)/(3+cos^2 ((x/2))))dx} =π ∫_0 ^π sinx(7/((3+sin^2 ((x/2)))(3+cos^2 ((x/2))))dx =7π ∫_0 ^π ((sinx)/((3+((1−cosx)/2))(3+((1+cosx)/2))))dx =28π∫_0 ^π sinx{(1/(7−cosx)) +(1/(7+cosx))}dx =28π { ∫_0 ^π ((sinx)/(7−cosx))dx +∫_0 ^π ((sinx)/(7 +cosx))dx} =28π{ [ln∣7−cosx∣]_0 ^π −[ln∣7+cosx∣]_0 ^π } =28π{ ln(8)−ln(6)−ln(6) +ln(8)} =28π{2ln(8)−2ln(6)} =56π{ln(8)−ln(6)} =56π{3ln(2)−ln(2)−ln(3)} ⇒ A =56π{2ln(2)−ln(3)} .](Q62992.png) | ||
Answered by Hope last updated on 27/Jun/19 | ||
 | ||
| ||