
Question and Answers Forum
Question Number 65320 by hovea cw last updated on 28/Jul/19
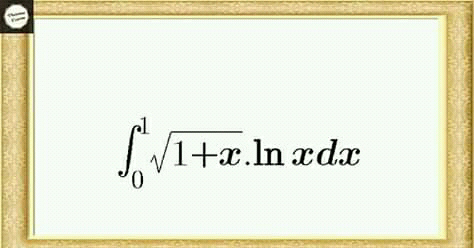
Commented by mathmax by abdo last updated on 28/Jul/19
![let I =∫_0 ^1 (√(1+x))lnxdx changement (√(1+x))=t give 1+x =t^2 ⇒ x =t^2 −1 and I =∫_1 ^(√2) tln(t^2 −1)(2t)dt =2 ∫_1 ^(√2) t^2 ln(t^2 −1)dt by parts u^′ =t^2 and v =ln(t^2 −1) ⇒ ∫_1 ^(√2) t^2 ln(t^2 −1)dt =[((t^3 /3)−(1/3))ln(t^2 −1)]_1 ^(√2) −∫_1 ^(√2) (((t^3 −1)/3))((2t)/(t^2 −1))dt =(((2(√2))/3)−(1/3))×0 −lim_(t→1) ((t^3 −1)/3)ln(t^2 −1)−(2/3) ∫_1 ^(√2) ((t^4 −t)/(t^2 −1))dt =0−0 −(2/3) ∫_1 ^(√2) ((t^4 −t)/(t^2 −1))dt ∫_1 ^(√2) ((t^4 −t)/(t^2 −1))dt =∫_1 ^(√2) ((t(t^3 −1))/(t^2 −1))dt =∫_1 ^(√2) ((t(t−1)(t^2 +t+1))/((t−1)(t+1)))dt =∫_1 ^(√2) ((t^3 +t^2 +t)/(t+1)) dt =∫_1 ^(√2) ((t^2 (t+1)−t^2 +t^2 +t)/(t+1))dt =∫_1 ^(√2) t^(2 ) dt +∫_1 ^(√2) ((tdt)/(t+1)) =[(t^3 /3)]_1 ^(√2) +∫_1 ^(√2) (1−(1/(t+1)))dt =((2(√2))/3)−(1/3) +(√2)−1 −[ln∣t+1∣]_1 ^(√2) =(5/3)(√2)−(4/3) −ln(1+(√2))+ln(2) ⇒ I =−(4/3){(5/3)(√2)−(4/3) +ln((2/(1+(√2))))} I =−((20)/9)(√(2 )) +((16)/9) −(4/3)ln((2/(1+(√2))))](Q65337.png)
| ||
Question and Answers Forum | ||
Question Number 65320 by hovea cw last updated on 28/Jul/19 | ||
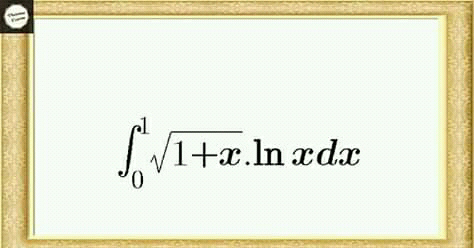 | ||
Commented by mathmax by abdo last updated on 28/Jul/19 | ||
![let I =∫_0 ^1 (√(1+x))lnxdx changement (√(1+x))=t give 1+x =t^2 ⇒ x =t^2 −1 and I =∫_1 ^(√2) tln(t^2 −1)(2t)dt =2 ∫_1 ^(√2) t^2 ln(t^2 −1)dt by parts u^′ =t^2 and v =ln(t^2 −1) ⇒ ∫_1 ^(√2) t^2 ln(t^2 −1)dt =[((t^3 /3)−(1/3))ln(t^2 −1)]_1 ^(√2) −∫_1 ^(√2) (((t^3 −1)/3))((2t)/(t^2 −1))dt =(((2(√2))/3)−(1/3))×0 −lim_(t→1) ((t^3 −1)/3)ln(t^2 −1)−(2/3) ∫_1 ^(√2) ((t^4 −t)/(t^2 −1))dt =0−0 −(2/3) ∫_1 ^(√2) ((t^4 −t)/(t^2 −1))dt ∫_1 ^(√2) ((t^4 −t)/(t^2 −1))dt =∫_1 ^(√2) ((t(t^3 −1))/(t^2 −1))dt =∫_1 ^(√2) ((t(t−1)(t^2 +t+1))/((t−1)(t+1)))dt =∫_1 ^(√2) ((t^3 +t^2 +t)/(t+1)) dt =∫_1 ^(√2) ((t^2 (t+1)−t^2 +t^2 +t)/(t+1))dt =∫_1 ^(√2) t^(2 ) dt +∫_1 ^(√2) ((tdt)/(t+1)) =[(t^3 /3)]_1 ^(√2) +∫_1 ^(√2) (1−(1/(t+1)))dt =((2(√2))/3)−(1/3) +(√2)−1 −[ln∣t+1∣]_1 ^(√2) =(5/3)(√2)−(4/3) −ln(1+(√2))+ln(2) ⇒ I =−(4/3){(5/3)(√2)−(4/3) +ln((2/(1+(√2))))} I =−((20)/9)(√(2 )) +((16)/9) −(4/3)ln((2/(1+(√2))))](Q65337.png) | ||