Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 65884 by Sayantan chakraborty last updated on 05/Aug/19

Commented by Sayantan chakraborty last updated on 05/Aug/19

$$\mathrm{answer}\mathrm{is}\mathrm{unknown}\mathrm{to}\mathrm{me}$$

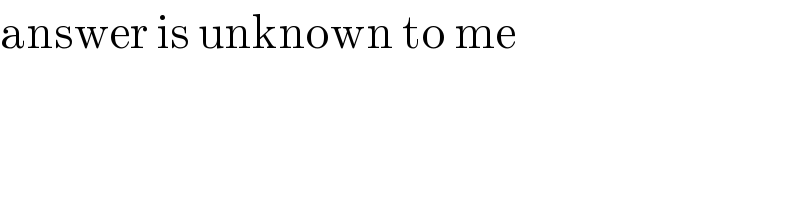
Commented by Tony Lin last updated on 06/Aug/19

$$let\mathrm{\angle }BAD=\mathrm{\angle }BCD=\theta ,\mathrm{\angle }BDA=\mathrm{\varnothing }$$$$\frac{5}{sin\mathrm{\varnothing }}=\frac{6sin\theta }{sin\theta }=6$$$$\Rightarrow sin\mathrm{\varnothing }=\frac{5}{6},cos\mathrm{\varnothing }=-\frac{\sqrt{11}}{6}$$$$2({DM}^2+{AM}^2)={DC}^2+{AD}^2$$$${DC}^2={\left(6cos\theta \right)}^2=36{cos}^2\theta$$$$\frac{AD}{sin(180°-\theta -\mathrm{\varnothing })}=\frac{6sin\theta }{sin\theta }=6$$$$AD=6sin(\theta +\mathrm{\varnothing })=5cos\theta -\sqrt{11}sin\theta$$$${AD}^2=25{cos}^2\theta -10\sqrt{11}sin\theta cos\theta +11{sin}^2\theta$$$${AC}^2=5^2+6^2-2\times 5\times 6cos(270°-2\theta -\mathrm{\varnothing })$$$$=61+60sin(2\theta +\mathrm{\varnothing })$$$$=61+60[2sin\theta cos\theta cos\mathrm{\varnothing }+(1-2{sin}^2\theta )sin\mathrm{\varnothing }]$$$$=61-20\sqrt{11}sin\theta cos\theta +50-100{sin}^2\theta$$$${AM}^2=\frac{61}{4}-5\sqrt{11}sin\theta cos\theta +\frac{25}{2}-25{sin}^2\theta$$$$2({DM}^2+{AM}^2)={DC}^2+{AD}^2$$$$2{DM}^2+\frac{61}{2}-10\sqrt{11}sin\theta cos\theta +25-50{sin}^2\theta$$$$=36{cos}^2\theta +25{cos}^2\theta -10\sqrt{11}sin\theta cos\theta +11{sin}^2\theta$$$$2{DM}^2+\frac{61}{2}+25=61({sin}^2\theta +{cos}^2\theta )$$$${DM}^2=\frac{11}{4}\Rightarrow DM=\frac{\sqrt{11}}{2}=\frac{\sqrt{a}}{2}$$$$\Rightarrow a=11$$

Commented by Sayantan chakraborty last updated on 17/Aug/19

$$\mathbf{sir}\mathbf{please}\mathbf{solve}\mathbf{question}\mathbf{number}65886$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com