Math Question and Answers


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 67516 by LPM last updated on 28/Aug/19

Commented by Prithwish sen last updated on 28/Aug/19

$\cos^{2} x + {({2 \cos}^{2} x - 1)}^{2} = 1 - \cos^{2} 3 x$ $Simplyfying we get,$ ${2 \cos}^{2} x ({4 \cos}^{4} x - {10 \cos}^{2} x + 3) = 0$ $\Rightarrow \cos^{2} x = 0 and \cos^{2} x = \frac{10 \pm \sqrt{52}}{8}$ $∴ x = (2 n - 1) \frac{π}{2} and x = {Cos}^{- 1} [\frac{\sqrt{5 \pm \sqrt{13}}}{2}]$ $please check .$
Commented by mathmax by abdo last updated on 19/Sep/19
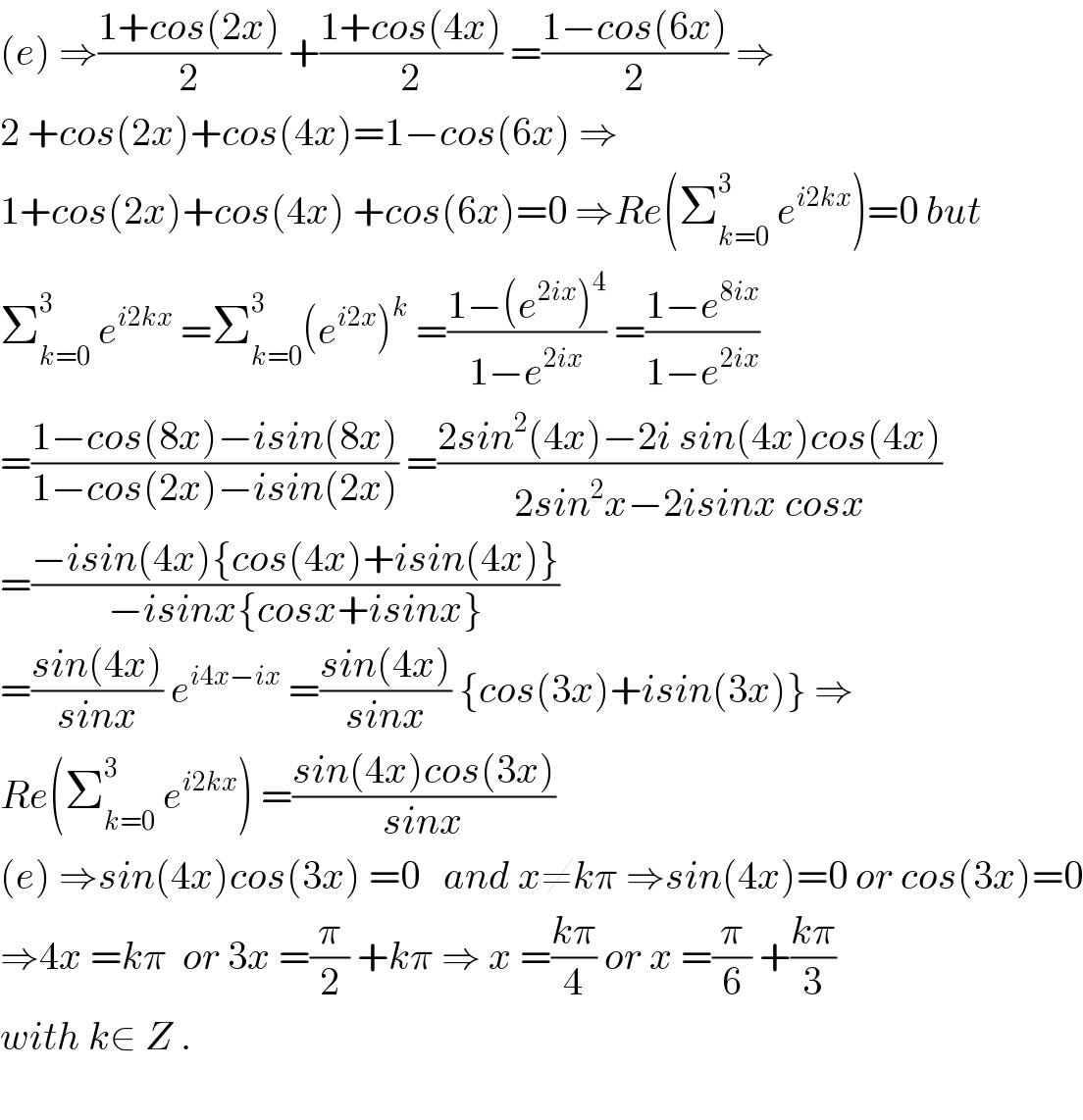
$(e) ⇒((1+cos(2x))/2) +((1+cos(4x))/2) =((1−cos(6x))/2) ⇒ 2 +cos(2x)+cos(4x)=1−cos(6x) ⇒ 1+cos(2x)+cos(4x) +cos(6x)=0 ⇒Re(Σ_(k=0) ^3 e^(i2kx) )=0 but Σ_(k=0) ^3 e^(i2kx) =Σ_(k=0) ^3 (e^(i2x) )^k =((1−(e^(2ix) )^4 )/(1−e^(2ix) )) =((1−e^(8ix) )/(1−e^(2ix) )) =((1−cos(8x)−isin(8x))/(1−cos(2x)−isin(2x))) =((2sin^2 (4x)−2i sin(4x)cos(4x))/(2sin^2 x−2isinx cosx)) =((−isin(4x){cos(4x)+isin(4x)})/(−isinx{cosx+isinx})) =((sin(4x))/(sinx)) e^(i4x−ix) =((sin(4x))/(sinx)) {cos(3x)+isin(3x)} ⇒ Re(Σ_(k=0) ^3 e^(i2kx) ) =((sin(4x)cos(3x))/(sinx)) (e) ⇒sin(4x)cos(3x) =0 and x≠kπ ⇒sin(4x)=0 or cos(3x)=0 ⇒4x =kπ or 3x =(π/2) +kπ ⇒ x =((kπ)/4) or x =(π/6) +((kπ)/3) with k∈ Z .$
$(e) \Rightarrow \frac{1 + c o s (2 x)}{2} + \frac{1 + c o s (4 x)}{2} = \frac{1 - c o s (6 x)}{2} \Rightarrow$ $2 + c o s (2 x) + c o s (4 x) = 1 - c o s (6 x) \Rightarrow$ $1 + c o s (2 x) + c o s (4 x) + c o s (6 x) = 0 \Rightarrow R e (\sum_{k = 0}^{3} e^{i 2 k x}) = 0 b u t$ $\sum_{k = 0}^{3} e^{i 2 k x} = \sum_{k = 0}^{3} {(e^{i 2 x})}^{k} = \frac{1 - {(e^{2 i x})}^{4}}{1 - e^{2 i x}} = \frac{1 - e^{8 i x}}{1 - e^{2 i x}}$ $= \frac{1 - c o s (8 x) - i s i n (8 x)}{1 - c o s (2 x) - i s i n (2 x)} = \frac{2 {s i n}^{2} (4 x) - 2 i s i n (4 x) c o s (4 x)}{2 {s i n}^{2} x - 2 i s i n x c o s x}$ $= \frac{- i s i n (4 x) {c o s (4 x) + i s i n (4 x)}}{- i s i n x {c o s x + i s i n x}}$ $= \frac{s i n (4 x)}{s i n x} e^{i 4 x - i x} = \frac{s i n (4 x)}{s i n x} {c o s (3 x) + i s i n (3 x)} \Rightarrow$ $R e (\sum_{k = 0}^{3} e^{i 2 k x}) = \frac{s i n (4 x) c o s (3 x)}{s i n x}$ $(e) \Rightarrow s i n (4 x) c o s (3 x) = 0 a n d x \neq k π \Rightarrow s i n (4 x) = 0 o r c o s (3 x) = 0$ $\Rightarrow 4 x = k π o r 3 x = \frac{π}{2} + k π \Rightarrow x = \frac{k π}{4} o r x = \frac{π}{6} + \frac{k π}{3}$ $w i t h k \in Z .$
	Answered by MJS last updated on 18/Sep/19
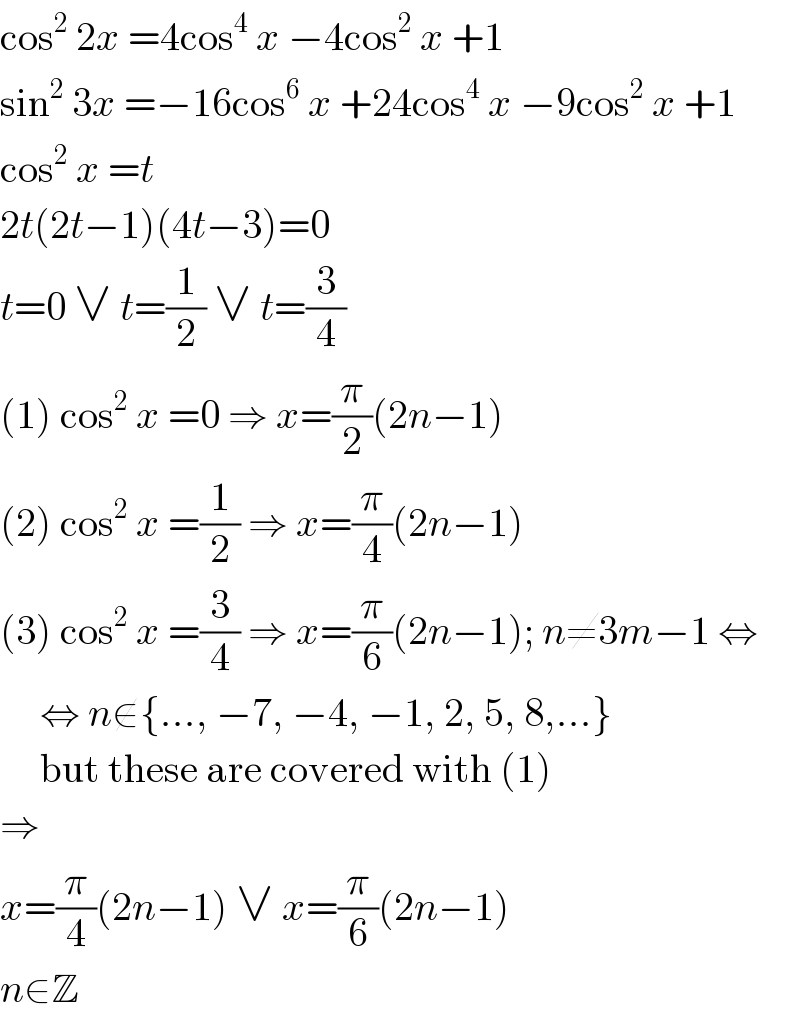
	$cos^2 2x =4cos^4 x −4cos^2 x +1 sin^2 3x =−16cos^6 x +24cos^4 x −9cos^2 x +1 cos^2 x =t 2t(2t−1)(4t−3)=0 t=0 ∨ t=(1/2) ∨ t=(3/4) (1) cos^2 x =0 ⇒ x=(π/2)(2n−1) (2) cos^2 x =(1/2) ⇒ x=(π/4)(2n−1) (3) cos^2 x =(3/4) ⇒ x=(π/6)(2n−1); n≠3m−1 ⇔ ⇔ n∉{..., −7, −4, −1, 2, 5, 8,...} but these are covered with (1) ⇒ x=(π/4)(2n−1) ∨ x=(π/6)(2n−1) n∈Z$
	$\cos^{2} 2 x = {4 \cos}^{4} x - {4 \cos}^{2} x + 1$ $\sin^{2} 3 x = - {16 \cos}^{6} x + {24 \cos}^{4} x - {9 \cos}^{2} x + 1$ $\cos^{2} x = t$ $2 t (2 t - 1) (4 t - 3) = 0$ $t = 0 \lor t = \frac{1}{2} \lor t = \frac{3}{4}$ $(1) \cos^{2} x = 0 \Rightarrow x = \frac{π}{2} (2 n - 1)$ $(2) \cos^{2} x = \frac{1}{2} \Rightarrow x = \frac{π}{4} (2 n - 1)$ $(3) \cos^{2} x = \frac{3}{4} \Rightarrow x = \frac{π}{6} (2 n - 1); n \neq 3 m - 1 \Leftrightarrow$ $\Leftrightarrow n \notin {. . ., - 7, - 4, - 1, 2, 5, 8, . . .}$ $but these are covered with (1)$ $\Rightarrow$ $x = \frac{π}{4} (2 n - 1) \lor x = \frac{π}{6} (2 n - 1)$ $n \in Z$
	Commented by Prithwish sen last updated on 28/Aug/19

	$thank you sir .$
	Answered by mr W last updated on 28/Aug/19

	$l e t t = \cos^{2} x ⩾ 0$ $\sin^{2} 3 x = (1 - \cos^{2} x) {(4 \cos^{2} x - 1)}^{2} = (1 - t) {(4 t - 1)}^{2}$ $\cos^{2} 2 x = {(2 \cos^{2} x - 1)}^{2} = {(2 t - 1)}^{2}$ $t + {(2 t - 1)}^{2} = (1 - t) {(4 t - 1)}^{2}$ $t (8 t^{2} - 10 t + 3) = 0$ $\Rightarrow t = 0, \frac{1}{2}, \frac{3}{4}$ $w i t h \cos^{2} x = 0 :$ $\Rightarrow x = n π \pm \frac{π}{2}$ $w i t h \cos^{2} x = \frac{1}{2} :$ $\cos x = \pm \frac{\sqrt{2}}{2}$ $\Rightarrow x = n π \pm \frac{π}{4}$ $w i t h \cos^{2} x = \frac{3}{4} :$ $\cos x = \pm \frac{\sqrt{3}}{2}$ $\Rightarrow x = n π \pm \frac{π}{6}$
	Commented by Prithwish sen last updated on 28/Aug/19

	$thank you sir .$
	Commented by LPM last updated on 29/Aug/19

	$goood$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum