Question and Answers Forum
Question Number 67535 by mr W last updated on 28/Aug/19
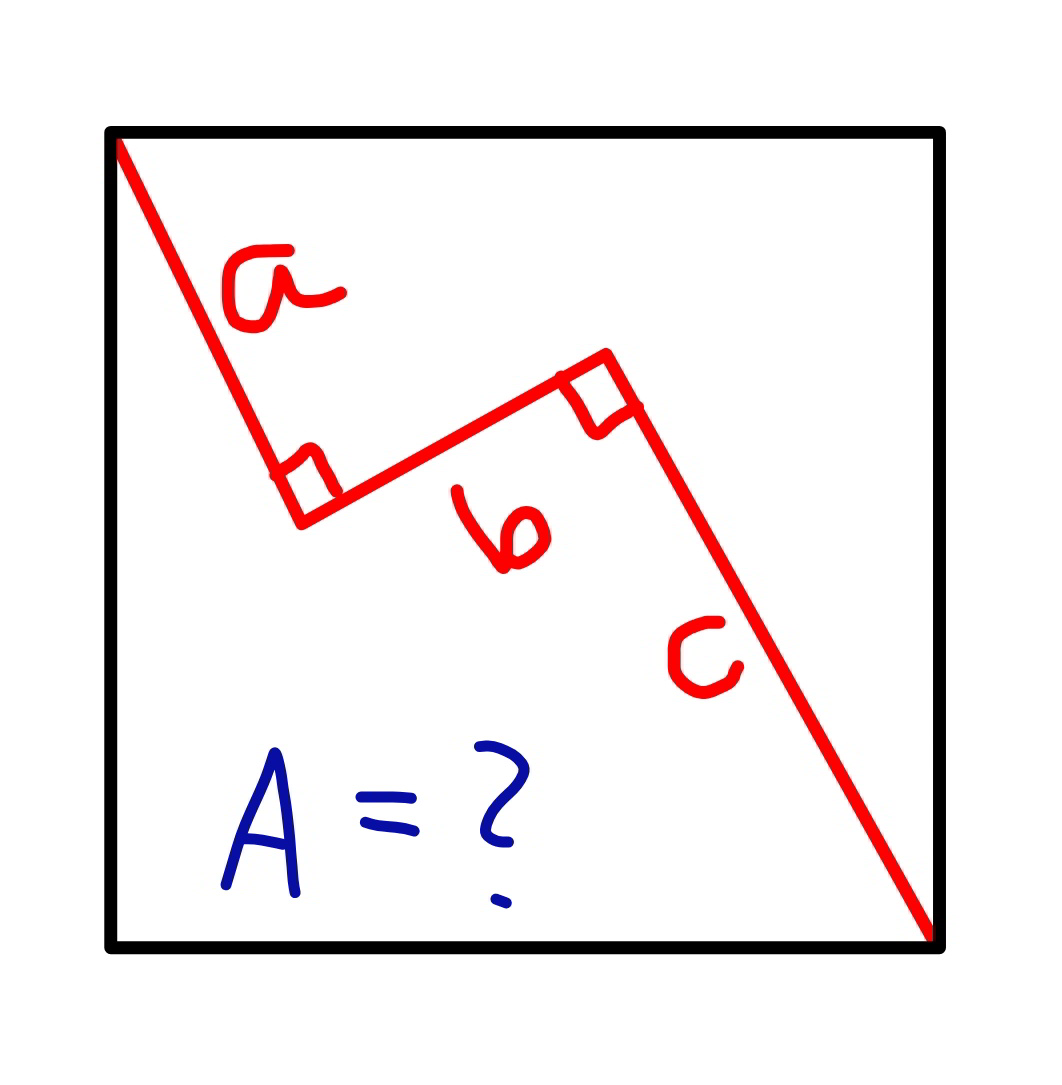
Commented by mr W last updated on 28/Aug/19
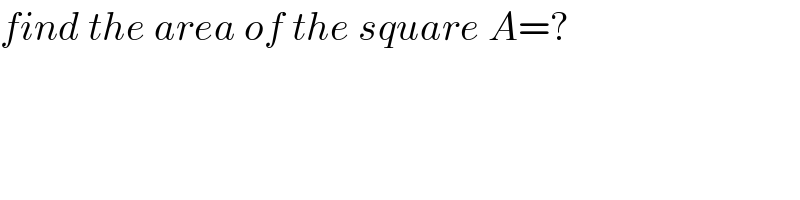
Commented by Prithwish sen last updated on 28/Aug/19

Commented by petrochengula last updated on 28/Aug/19
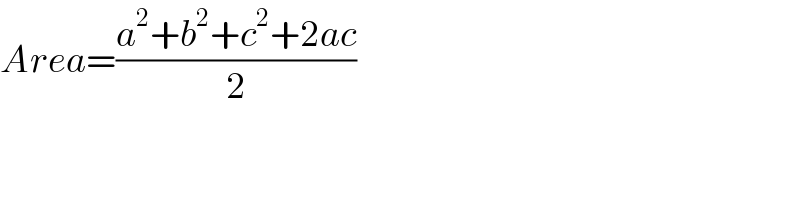
Commented by mr W last updated on 28/Aug/19
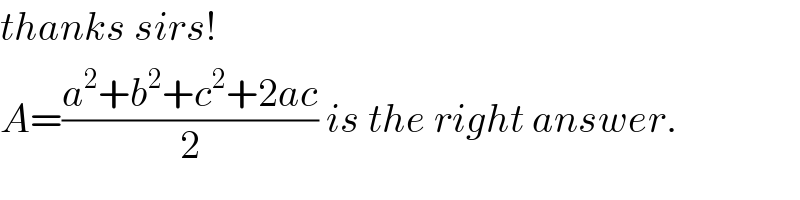
Commented by Prithwish sen last updated on 28/Aug/19
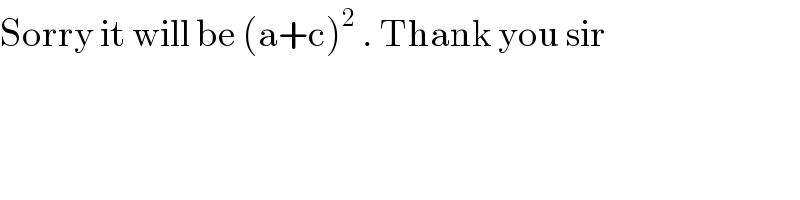
Answered by mr W last updated on 28/Aug/19
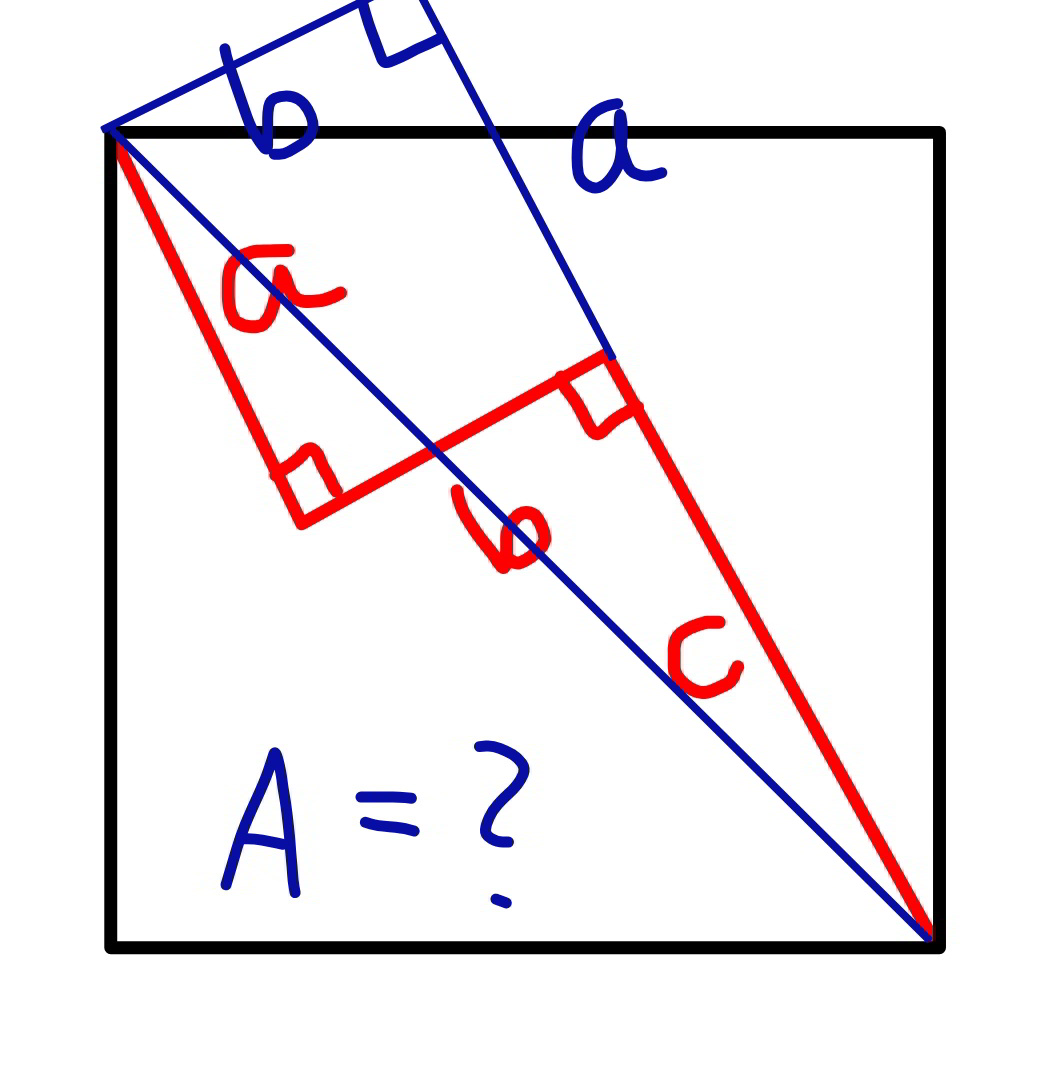
Commented by mr W last updated on 28/Aug/19
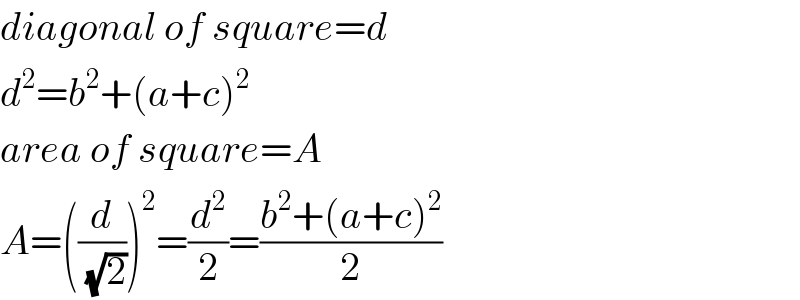
Commented by Prithwish sen last updated on 28/Aug/19

Commented by TawaTawa last updated on 28/Aug/19
Commented by Rasheed.Sindhi last updated on 28/Aug/19

Commented by mr W last updated on 28/Aug/19
Commented by Rasheed.Sindhi last updated on 29/Aug/19
سائين توھان جي مھرباني!Thanks s¡r
Commented by mr W last updated on 30/Aug/19

Commented by Rasheed.Sindhi last updated on 30/Aug/19

Commented by Rasheed.Sindhi last updated on 30/Aug/19
Sir, ich fühle mich mit Ihnen freundlicher als jeder andere Forum-Freund von mir.
Commented by mr W last updated on 30/Aug/19