
Question and Answers Forum
Question Number 67716 by TawaTawa last updated on 30/Aug/19

Answered by mind is power last updated on 30/Aug/19
![let c_1 =demi circle of r=2 c2=circle r=1 c_1 ..x^2 +y^2 =4 c_2 =x^2 +(y−h)^2 =1 withe (0,h) center of c_2 c_1 ∩c_2 ⇒y^2 −(y−h)^2 =3 ⇒2yh−h^2 =3⇒y=((3+h^2 )/(2h))=y_0 x^2 =(4−y^2 )=((16h^2 −(3+h^2 )^2 )/(4h^2 ))=((−h^4 +10h^2 −9)/(4h^2 ))=((−(h^2 −9)(h^2 −1))/(4h^2 )) ⇒h^2 ∈[1,9] either c_2 ∩c_1 ={} x=+_− (√((−(h^2 −9)(h^2 −1))/(4h^2 )))=+_− x_0 assum h^2 ∈[1.9] D(+x_0 .y_0 ).C=(−x_0 .y_0 ) DA+AB=∫_(−x_(0 ) ) ^(+x_0 ) (√(1+((dy/dx))^2 ))dx...c_1 (dy/dx)=d((√(4−x^2 )))/dx=((−x)/(√(4−x^2 )))⇒((dy/dx))^2 =(x^2 /(4−x^2 )) DA+AB=∫_(−x_0 ) ^(+x_0 ) (√(4/(4−x^2 )))dx x=2sin(δ)⇒dx=2cos(δ)dδ DA+AB=∫_(arcsin(−((x0)/2))) ^(arcsin(((x0)/2))) (√(4/(4−4sin^2 (δ)))).2cos(δ)dδ) =∫2.((2cos(δ))/(∣2cos(δ)∣))dδ=4∫_0 ^(arcsin((x_0 /2))) dδ=4arcsin((x_0 /2)) same idea too find DC+CB...](Q67727.png)
Commented by TawaTawa last updated on 30/Aug/19

Answered by mr W last updated on 30/Aug/19

Commented by mr W last updated on 30/Aug/19

Commented by TawaTawa last updated on 30/Aug/19
Commented by TawaTawa last updated on 30/Aug/19

Commented by TawaTawa last updated on 31/Aug/19

Commented by mr W last updated on 31/Aug/19

Commented by mr W last updated on 31/Aug/19
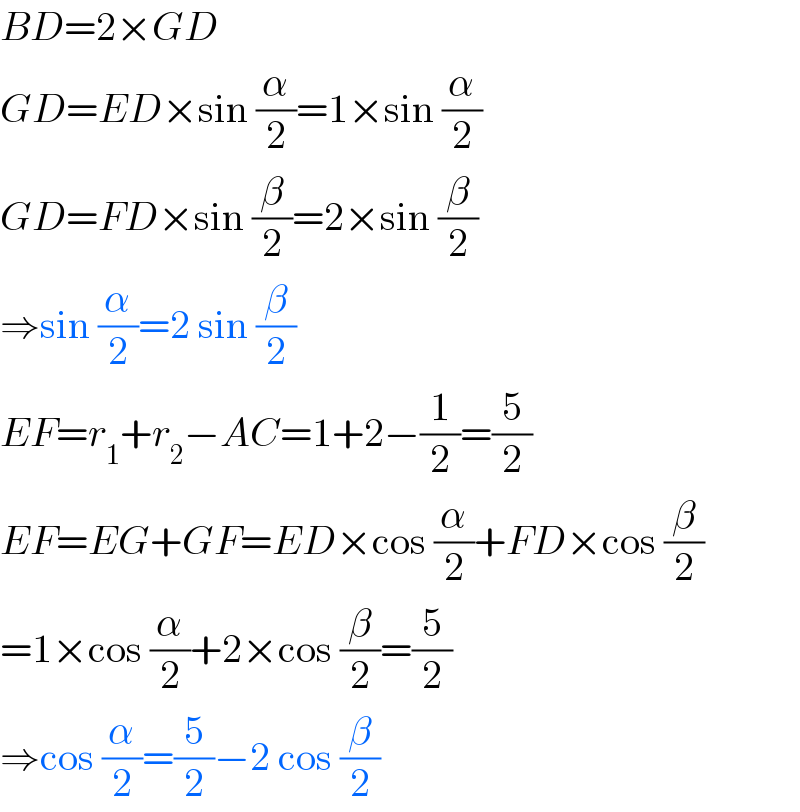
Commented by TawaTawa last updated on 31/Aug/19

