Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 67813 by mr W last updated on 31/Aug/19

Commented by mr W last updated on 31/Aug/19

$$shadedareaA=?$$

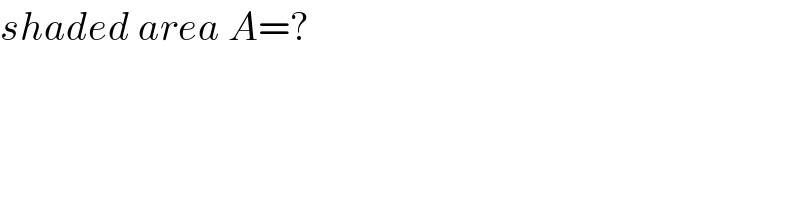
Commented by Prithwish sen last updated on 31/Aug/19

$${\mathrm{R}}_{\mathrm{A}}=13,{\mathrm{R}}_{\mathrm{B}}=6,{\mathrm{R}}_{\mathrm{C}}=5$$$$\mathrm{AB}=7,\mathrm{BC}=6+5=11,\mathrm{AC}=11-5=6$$$$\mathrm{s}=\frac{7+11+6}{2}=12$$$$\mathrm{Sin}\frac{\alpha }{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{AC})(\mathrm{s}-\mathrm{AB})}{\mathrm{AC}\times \mathrm{AB}}}=\sqrt{\frac{5}{7}}$$$$\mathit{\alpha }\backsim 115°$$$$\mathrm{Sin}\frac{\mathrm{ABC}}{2}=\sqrt{\frac{(12-7)(12-11)}{7\times 11}}\Rightarrow \mathit{\beta }\backsim 150°$$$$\mathrm{Sin}\frac{\mathrm{ACB}}{2}=\sqrt{\frac{(12-6)(12-11)}{6\times 11}}\Rightarrow \mathit{\gamma }\backsim 115°$$$$\mathbf{Area}\mathbf{of}△\mathbf{ABC}=\frac{1}{2}\mathrm{AB}\times \mathrm{AC}\times \sin \alpha \backsim 19.03..\left(\mathrm{i}\right)$$$$\mathbf{Area}\mathbf{of}\mathbf{the}\mathbf{sector}\mathbf{of}\mathbf{the}\mathbf{circle}\mathbf{C},$$$${\mathbf{S}}_{\mathbf{c}}=\mathit{\pi }{\left({\mathbf{R}}_{\mathbf{c}}\right)}^2\times \frac{115}{360}\backsim 25.08...\left(\mathrm{ii}\right)$$$$\mathbf{Smilarly}{\mathbf{S}}_{\mathbf{B}}=\mathit{\pi }{\left({\mathbf{R}}_{\mathbf{B}}\right)}^2\times \frac{150}{360}\backsim 47.12....\left(\mathrm{iii}\right)$$$$\mathbf{And}{\mathbf{S}}_{\mathbf{A}}=\mathit{\pi }{\left({\mathbf{R}}_{\mathbf{A}}\right)}^2\times \frac{115}{360}\backsim 169.6.....\left(\mathrm{iv}\right)$$$$\therefore \mathbf{Area}\mathbf{of}\mathbf{the}\mathbf{shadded}\mathbf{portion}$$$$=\left(\mathbf{iv}\right)-[\left(\mathbf{i}\right)+\left(\mathbf{ii}\right)+\left(\mathbf{iii}\right)]\backsim 78.37$$$$\mathbf{Sir}\mathbf{waiting}\mathbf{for}\mathbf{your}\mathbf{feedback}.$$

Commented by mr W last updated on 01/Sep/19

$${it}^{\prime }scorrectwaysir!$$$$butcheckthevalue:$$$$AC=13-5=8$$

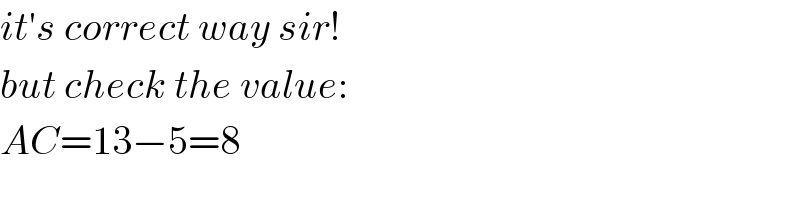
Commented by Prithwish sen last updated on 01/Sep/19

$$\mathrm{oh}!\mathrm{I}\mathrm{made}\mathrm{a}\mathrm{mistake}.$$

Commented by Rasheed.Sindhi last updated on 01/Sep/19

Sir prithwish sen please see my answer to Q#67697.There I have tried to apply Chinese Remainder Theorm in case of polynomials.Your critical remarks are important for me!

Commented by Prithwish sen last updated on 01/Sep/19

$$\mathrm{Sir}\mathrm{first}\mathrm{of}\mathrm{all}\mathrm{please}\mathrm{forgive}\mathrm{me}\mathrm{for}\mathrm{giving}$$$$\mathrm{delayed}\mathrm{response}.\mathrm{There}\mathrm{is}\mathrm{something}\mathrm{going}$$$$\mathrm{wrong}\mathrm{as}\mathrm{I}\mathrm{am}\mathrm{not}\mathrm{getting}\mathrm{any}\mathrm{notification}.$$$$\mathrm{So}\mathrm{it}\mathrm{is}\mathrm{my}\mathrm{request}\mathrm{to}\mathrm{the}\mathrm{developer}\mathrm{please}$$$$\mathrm{fix}\mathrm{it}.\mathrm{Now}\mathrm{back}\mathrm{to}\mathrm{the}\mathrm{problem}\mathrm{sir}\mathrm{you}\mathrm{have}$$$$\mathrm{done}\mathrm{a}\mathrm{wonderful}\mathrm{job}.\mathrm{I}\mathrm{dont}\mathrm{find}\mathrm{anything}$$$$\mathrm{wrong}\mathrm{in}\mathrm{your}\mathrm{solution}.\mathrm{Thanks}\mathrm{again}\mathrm{sir}.$$

Commented by Rasheed.Sindhi last updated on 02/Sep/19

$$\mathrm{TThhaannkkss}\mathrm{a}\mathrm{lot}\mathrm{sir}!$$$$\mathrm{Actually}\mathrm{I}{\mathrm{haven}}^{\prime }\mathrm{t}\mathrm{seen}\mathrm{use}\mathrm{of}\mathrm{the}\mathrm{theorm}\mathrm{in}$$$$\mathrm{polynomials}.\therefore \mathrm{I}\mathrm{was}\mathrm{not}\mathrm{confident}!$$$$\mathrm{thanx}\mathrm{again}\mathrm{sir}!$$

Commented by Prithwish sen last updated on 02/Sep/19

$$\mathrm{you}\mathrm{are}\mathrm{always}\mathrm{welcome}\mathrm{sir}.$$

Answered by Prithwish sen last updated on 31/Aug/19

Terms of Service

Privacy Policy

Contact: info@tinkutara.com